Question 4 - Blow-up Example

We investigate the blow-up behaviour of the following ODE:

$\begin{array}{rl} x'(t) &= x^2, \\ x(0) &= 1 \end{array}$

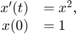
Contents

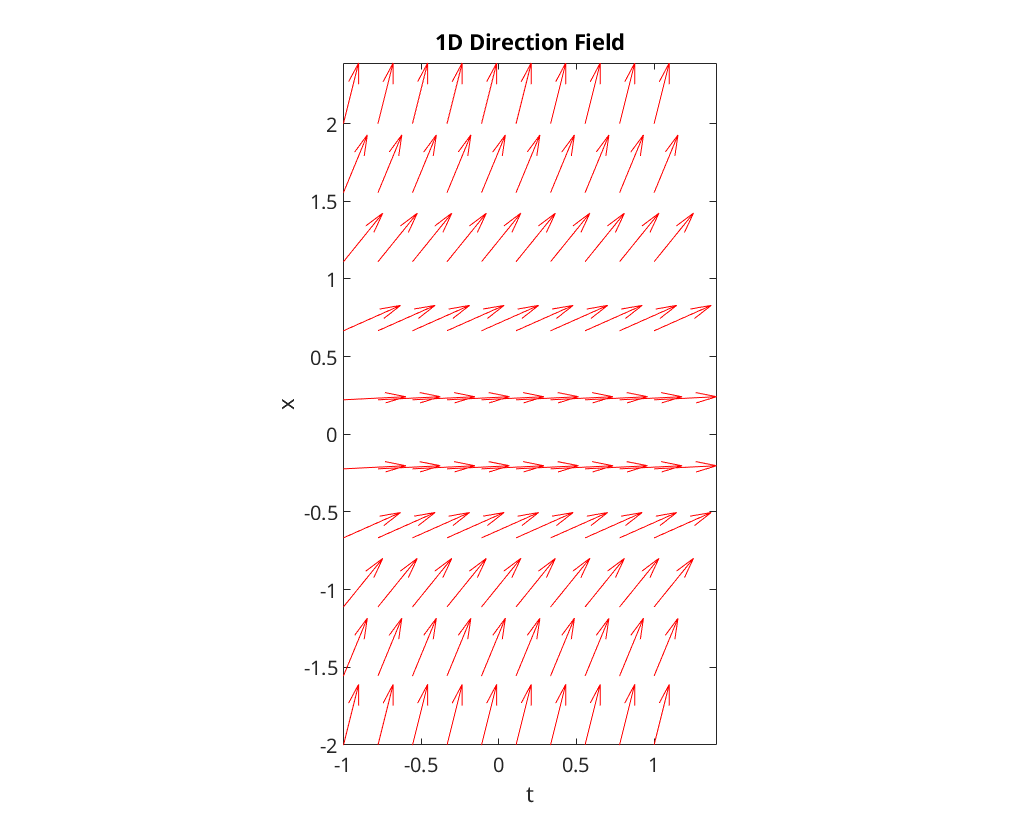
4(a) - Direction field

We first plot the direction field of the ODE over $t\in[-1,1]$ and $x\in[-2,2]$:

dirfield(@blowupex, -1, 1, -2, 2);

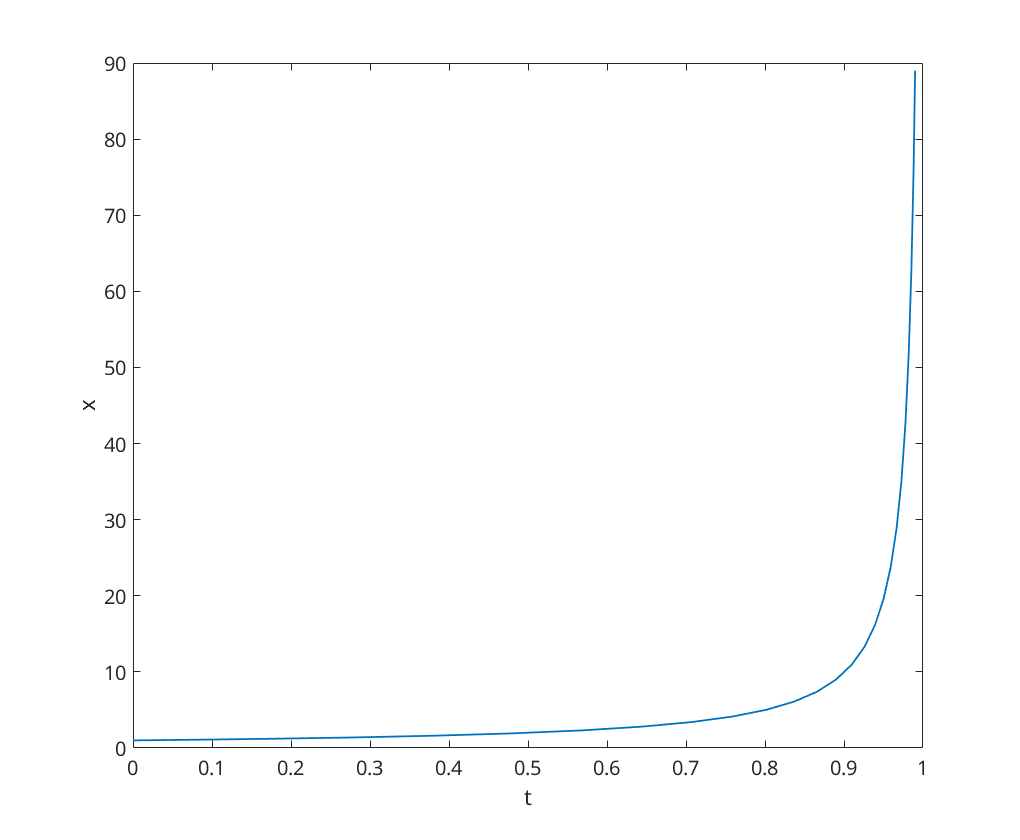
4(b) - Simulation over various time periods

We first simulate the ODE over the time period $t\in[0,0.99]$ (which stops before the blowup will occur)

[t,x] = ode23(@blowupex, [0, 0.99], 1);

figure;
plot(t, x);
xlabel('t');
ylabel('x');

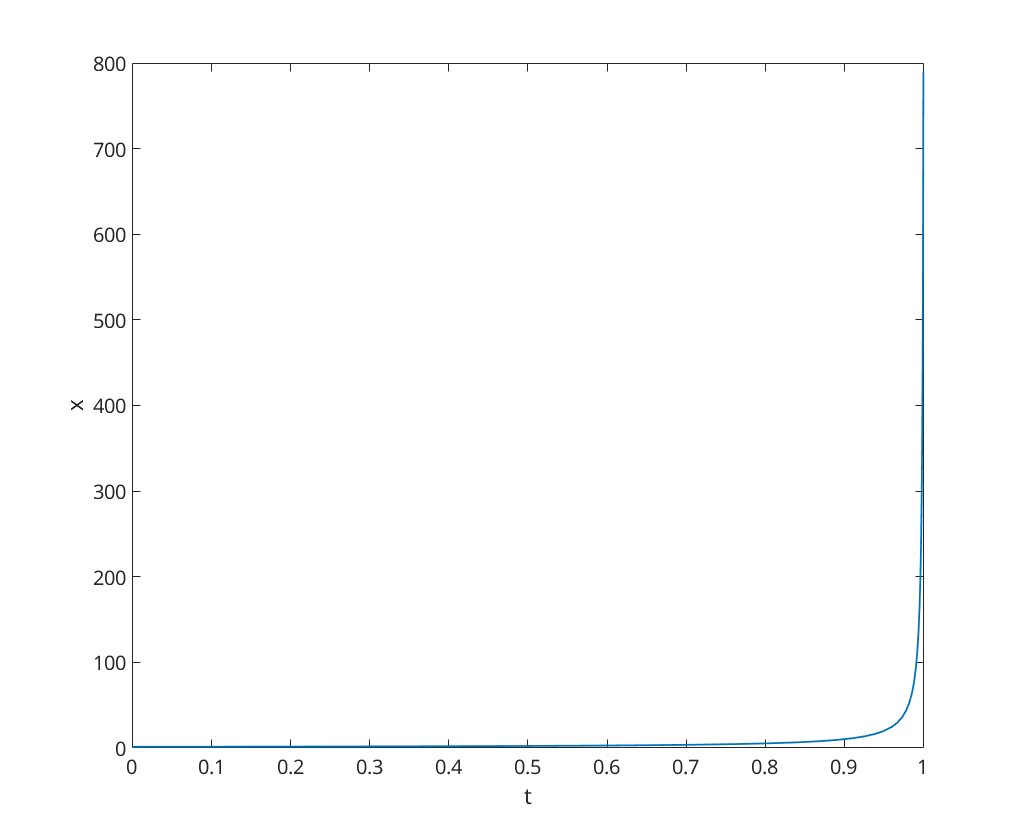
We now simulate the ODE over the time period $t\in[0,1]$

[t,x] = ode23(@blowupex, [0, 1], 1);

figure;
plot(t, x);
xlabel('t');
ylabel('x');

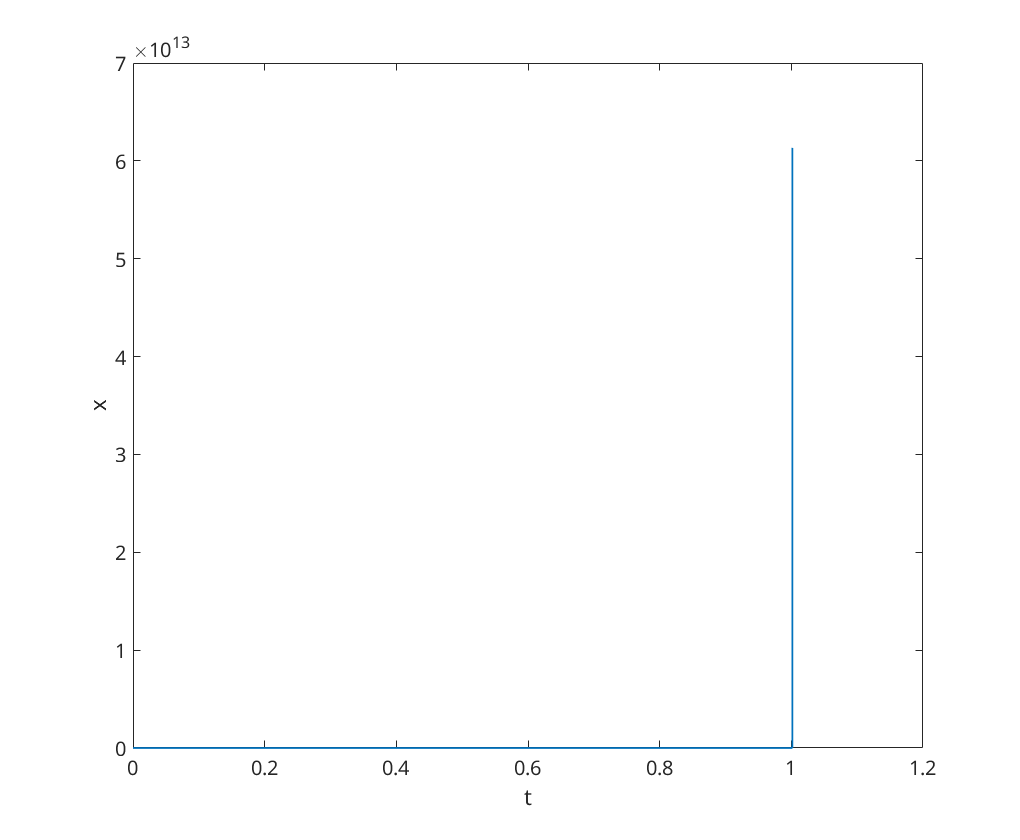
We now simulate the ODE over the time period $t\in[0,2]$ (which hits the blowup behaviour), we note that an error occurs when trying to solve

[t,x] = ode23(@blowupex, [0, 2], 1);

figure;
plot(t, x);
xlabel('t');
ylabel('x');

Warning: Failure at t=1.001616e+00.  Unable to meet integration tolerances
without reducing the step size below the smallest value allowed (3.552714e-15)
at time t. 

Published with MATLAB® R2023a