Warning: This page is about a course which took place in the winter semester 2015/2016. Please visit the homepage for up-to-date information.
Basic information
The contents of the course and other basic information are available in the Student Information System.
The schedule (to be found also in the Student Information System):
- lectures on Thursdays, 10.40am-12.10pm in room K5,
- problem sessions on Thursdays, 12.20pm-1.50pm in room K5.
Exam
The exam will be oral. Please contact me to agree on the date and time of your exam.
Credit
The credit will be granted for solved exercise problems. There will be three sets of the problems and they will appear here. Requested are at least 50% of successfully solved problems handed in withing the deadlines.
Problem set #1 (deadline for solutions: December 3)
- Let K be an algebraically closed field and I ⊆ K[x1, ..., xn] be an ideal. Show that the radical of I is equal to the intersection of the maximal ideals of K[x1, ..., xn] which contain I.
- Find generators of the maximal ideal M of the ring R[x,y] of polynomials over the real numbers which has zero at (2 + 3i,5 - 2i) ∈ A².
- Let C be the field of complex numbers and consider the ring R = C[x,y]/(xy) and the element f := x-y ∈ R. Show that the localized ring Rf (the element f is made invertible) is isomorphic to the ring C[x±1] × C[y±1].
Problem set #2 (deadline for solutions: December 17)
- A C-algebraic subset X ⊆ A2 is called a conic if it is of the form X = V({f(x,y)}) where f(x,y) is a non-zero polynomial of total degree 2. Show that every irreducible conic is isomorphic either to V({y-x2}) or to V({xy-1}).
- Let X = V({x3 + y3 - 3x2 - 3y2 +3xy +1}) be a plane curve defined over the field of complex numbers. Find all singular points of X and all tangent lines at these singular points.
- Show the variety X from the previous problem is birationally equivalent to the complex affine line.
Problem set #3 (deadline for solutions: January 14)
-
Let K be an algebraically closed field. We shall define a map i from the set of 2-dimesional subspaces V ⊆ K4 to the projective space P5 as follows. We arbitrarily choose two linearly independent vectors v = (a0, a1, a2, a3) and w = (b0, b1, b2, b3) in V, we write the components into a 2x4 matrix
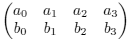
and we compute (in any fixed order) the 6 determinants d0, d1, ..., d5 of all 2x2 submatrices. Then we define i to map V to (d0 : d1 : ... : d5).
- Show that i is a well defined injective map.
- Show that the image G of i is a projective variety given in P5 by a single quadratic equation.
- Show that we can cover G (as an abstract variety) by 6 open subsets isomorphic to A4.
(Hint: Apply Gauss elimination to the 2x4 matrix.)
- Consider the 6-dimensional subspace V of C[x,y] consisting of all polynomials of total degree at most 2. Consider also the corresponding projective space P5 whose elements are lines in V. Show that the irreducible conics in the complex affine space A2 are parametrized by a Zariski open subset of P5.
What has been lectured
A brief overview of what has been taught in individual lectures, including references to the literature, can be found below.
- October 8, 2015
- Affine algebraic sets, the assignments V and I, Zariski topology, the decomposition of a noetherian topological space to irreducible components, algebraic varieties ([Ful], sec. 1.2, 1.3, 1.5, 6.1; [Ga], sec. 1.1).
- October 15, 2015
- The characterization of varieties via prime ideals, polynomial maps, the connection between polynomial maps and homomorphisms of coordinate rings ([Ful], sec. 1.5, 2.1, 2.2; [Ga], sec. 1.3).
- October 22, 2015
- Localization of rings, Weak Nullstellensatz, radical ideals ([Ful], sec. 2.2; [AM], ch. 3).
- November 5, 2015
- Hilbert's Nullstellensatz, a characterization of coordinate rings among algebras, maximal ideals of coordinate rings, the standard basis for the Zariski topology, a geometric interpretation of the localization K[X]f ([Ful], sec. 1.7, 6.1; [Ga], sec. 1.2, 2.1).
- November 12, 2015
- A geometric interpretation of the localization K[X]f (proved), regular functions and their description on basic Zariski open sets ([Ful], sec. 2.4; [Ga], sec. 1.2).
- November 26, 2015
- Description of OX(U) for basic Zariski open sets U (proved), local rings at points of an algebraic set ([Ful], sec. 2.4; [Ga], sec. 1.2).
- December 3, 2015
- Local rings at points of an algebraic set (continued), cotangent space ([Ful], sec. 2.4, 2.9; [Ga], sec. 2.1).
- December 10, 2015
- A characterization of non-singular points on plane curves, (non)singular points of algebraic sets in general, sheaves of K-algebras, ringed spaces ([Ful], sec. 3.1, 3.2; [Ga], sec. 2.2, 4.4).
- December 17, 2015
- Homomorphisms of ringed spaces, affine open sets, abstract algebraic sets ([Ga], sec. 2.3 - 2.5; [Nee], chap. 2).
- January 7, 2016
- Abstract algebraic sets and the criterion on the diagonal Δ(X) of X x X, projective algebraic sets, projective Nullstellensatz, projective algebraic sets as abstract algebraic sets ([Ful], sec. 4.1, 4.2; [Ga], sec. 2.5, 3.1 - 3.3).
- January 14, 2016
- Closedness of morphisms whose domain is a projective algebraic set, the Krull dimension and a sketch of a computation of the dimension for projective and affine spaces ([Ga], sec. 3.4, 4.1, 4.2).
Literature
Algebraic geometry is a very broad field with thousands of pages written about it from several points of view. To get an impression (or to get an idea where to go next for those interested in the topic), check this blog on mathoverflow.net. The core of the lecture is presented according to the following sources available in PDF:
| [Ga] | A. Gathmann, Algebraic geometry, notes from a course in Kaiserslautern, 2002/2003. [Full text in PDF] |
| [Ful] | W. Fulton, Algebraic Curves (An Introduction to Algebraic Geometry), 2008. [Full text in PDF] |
The lectures may also involve facts from the following (off-line) sources:
| [Sh] | I. R. Shafarevich, Basic algebraic geometry 1, Varieties in projective space, 2. vyd., Springer-Verlag, Berlin, 1994. |
| [AM] | M. F. Atiyah, I. G. MacDonald, Introduction to Commutative Algebra, Addison-Wesley Publishing Co., 1969. |
| [CLO] | D. Cox, J. Little, D. O'Shea, Ideals, varieties, and algorithms, Second Edition, Springer, New York, 2005. |
| [Na] | M. Nagata, Local Rings, John Wiley & Sons, 1962. |