Sjednocení množin
Další operace, kterou si ukážeme, slouží ke „spojení“ dvou množin. Tato operace se jmenuje sjednocení a značíme ji „\(\cup\)“. Definice je následující:
Množina \(A\cup B\) obsahuje jen a pouze takové prvky, které patří alespoň do jedné z množin \(A\) a \(B\).
Sjednocením dvou množin tedy získáme množinu, která obsahuje všechny prvky z obou těchto množin. Zkrátka „sesypeme“ obě množiny do jedné, nesmíme však zapomenout, že množina nemůže obsahovat více exemplářů stejného prvku (pokud je tedy nějaký prvek v obou množinách, v jejich sjednocení bude pouze jednou)!
Grafické znázornění sjednocení množin je následující:
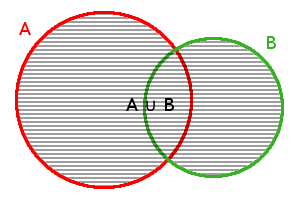
\(A\cup B\)
Nyní se opět podívejme na několik konkrétních příkladů sjednocení:
- Uvažujme nějakou třídu 1.A. Nechť množinou \(Ch\) je množina všech chlapců z této třídy a množinou \(D\) je množina všech dívek z téže třídy. Pak množina \(D\cup Ch\) je množina všech studentů a studentek třídy 1.A.
- Mějme množiny \(A\) = {1, 2, 3, 4, 5, 6} a \(B\) = {3, 6, 8, 9}. Pak je množina \(A\cup B\) = {1, 2, 3, 4, 5, 6, 8, 9}.
- Mějme množiny \(A\) = {1, 2, 3, 4, 5, 6} a \(B\) = \(\emptyset\). Pak je množina \(A\cup B\) = {1, 2, 3, 4, 5, 6}. Platí to i obecně, pro jakoukoli množinu \(M\) je \(M\cup \emptyset\) = \(M\).
- Předchozí příklad můžeme ještě více zobecnit. Uvažujme množiny \(C\) a \(D\), pro něž platí \(C \subseteq D\). Pak \(C\cup D\) = \(D\). Tedy sjednocením množiny a její podmnožiny je vždy původní množina.
- Stejně tak získáme původní množinu, pokud ji sjednotíme se sebou samou: \(M\cup M\) = \(M\).
Jak je to s komutativitou sjednocení množin? Z jeho definice plyne, že tato operace je komutativní, sléváme prvky z obou množin do jedné a nezáleží nám na tom, kterou začneme. Zkráceně můžeme zapsat tento poznatek následovně: Pro každé dvě množiny \(A\) a \(B\) platí, že \(A\cup B\) = \(B\cup A\).
