Příklady řešené s využitím Vennových diagramů
Příklady, které si ukážeme, je možné řešit i bez Vennových diagramů, my si ale ukážeme, jak nám tyto diagramy mohou řešení ulehčit a zjednodušit.
Příklad 1
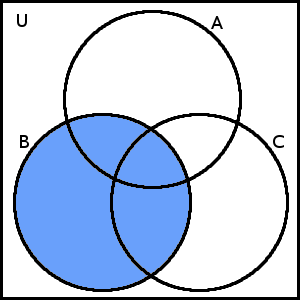
Malá firma má 25 zaměstnanců, z toho 12 zaměstnanců má řidičský průkaz, 8 zaměstanců má svářečský průkaz. 10 zaměstnanců nevlastní ani jeden z těchto průkazů. Kolik zaměstnanců firmy má svářečský i řidičský průkaz zároveň?
Za základní množinu \(U\) vezmeme množinu všech zaměstnanců firmy. Je zřejmé, že \(|U|\) = 25. Dále budeme uvažovat množinu \(Ř\) všech zaměstnanců vlastnících řidičský průkaz a množinu \(S\) všech zaměstanců, kteří mají svářečský průkaz. Platí tedy \(|Ř|\) = 12 a \(|S|\) = 8. Teď vše zakresleme do Vennova diagramu:
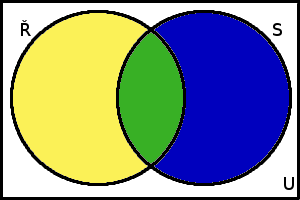
Vennův diagram k Příkladu 1
Proberme si, co reprezentují jednotlivé části diagramu. Množina \(Ř\) je zde složena ze dvou částí – žluté a zelené, množina \(S\) je složena ze zelené a modré. Zelená část označuje množinu \(Ř \cap S\), což je množina zaměstnanců, kteří mají současně řidičský i svářečský průkaz. Mohutnost této množiny je pro nás klíčová, je totiž řešením úlohy. Zatím ji však neznáme. Je zde však jedna množina, jejíž mohutnost známe a jíž jsme zatím nezmínili. Jakou množinu reprezentuje bílá část diagramu? Je to množina (\(Ř\cup S\))', jinak ji můžeme zapsat také jako \(U\) − (\(Ř\cup S\)). To je množina zaměstnanců, kteří nevlastní ani jeden z průkazů. Její mohutnost ze zadání známe, ta je 10. Deset zaměstanců tedy spadá do „bílé části“ diagramu, zbývajících 15 musí být v „barevné části“. Co je vlastně ona barevná část? To je množina \(Ř\cup S\) neboli množina všech zaměstnanců, kteří vlastní alespoň jeden z průkazů. Dokážeme již nyní určit, kolik zaměstnanců vlastní oba průkazy?
Víme, že \(|Ř\cup S|\) = 15, a také víme, že \(|Ř|\) = 12 a \(|S|\) = 8. Sjednocení množin obsahuje 15 prvků, součet počtů prvků množin \(Ř\) a \(S\) je však 12 + 8 = 20. Z toho je zřejmé, že tyto množiny musí mít několik společných prvků – konkrétně je to 20 − 15, tedy 5 prvků. Neboli \(|Ř \cap S|\) = 5. Množina \(Ř \cap S\) je právě ona zelená část diagramu, neboli množina zaměstnanců vlastnících oba průkazy. Oba průkazy tedy vlastní 5 zaměstnanců.
Příklad 2
Do hudební školy chodí 200 žáků. 80 žáků hraje na housle nebo na klavír, 189 žáků hraje na nejvýše jeden z těchto nástrojů. Na klavír hraje o 13 žáků víc než na housle. Kolik žáků hraje na oba nástroje a kolik klavíristů nehraje na housle?
Základní množinou \(U\) bude tentokrát množina všech žáků navštěvujících hudební školu. Dále označme \(K\) množinu všech tamějších klavíristů a \(H\) množinu všech houslistů navštěvujících školu. A zakresleme vše do Vennova diagramu:
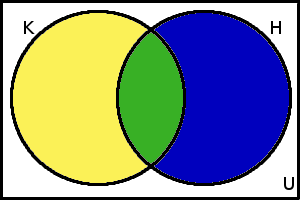
Vennův diagram k Příkladu 2
Co obsahují jednotlivé barevně vyznačené množiny? Žlutá značí žáky, kteří chodí na klavír, ale nehrají na housle. Modrá naopak značí houslisty, kteří nechodí na klavír. Zelená potom označuje ty, kteří hrají na oba nástroje, tj. množinu \(K \cap H\). Žlutá a zelená dohromady značí množinu \(K\), modrá a zelená pak množinu \(H\). Bílá část diagramu značí množinu žáků, kteří nehrají ani na jeden z těchto nástrojů.
Shrňme si, co víme ze zadání. Do školy chodí celkem 200 žáků, tj. \(|U|\) = 200. Dále víme, že 80 žáků hraje na klavír nebo na housle (pozor, spojka nebo zde není ve smyslu vylučovacím, tento počet tak zahrnuje i žáky, kteří hrají na oba nástroje). Tedy platí \(|K\cup H|\) = 80. Také víme, že \(|K|\) = \(|H|\) + 13. Jakou část diagramu zachycuje 189 žáků, kteří chodí nejvýše na jeden ze zmiňovaných nástrojů? Jsou to vlastně všichni žáci, kteří navštěvují školu ale zároveň nehrají na oba nástroje. To znamená, chceme-li tuto množinu zachytit (v našem případě šrafováním), bude zabírat celý diagram kromě množiny \(K \cap H\):
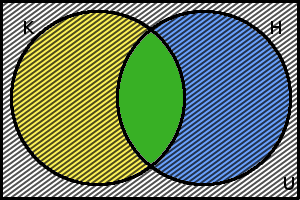
Doplněný Vennův diagram k Příkladu 2
Pro jistotu si naše dosavadní poznatky ještě shrňme do tabulky:
| Množina | Mohutnost | Vyznačení v diagramu |
|---|---|---|
| \(U\) | 200 | celá plocha diagramu |
| \(K\) | \(|H|\) + 13 | žlutá + zelená |
| \(H\) | ??? | modrá + zelená |
| \(K\cup H\) | 80 | žlutá + zelená + modrá |
| \(K \cap H\) | ??? | zelená |
| \(K\) − (\(K \cap H\)) | ??? | žlutá |
| \(H\) − (\(K \cap H\)) | ??? | modrá |
| \(U\) − (\(K\cup H\)) neboli (\(K\cup H\))' | ??? | bílá |
| \(U\) − (\(K \cap H\)) neboli (\(K \cap H\))' | 189 | šrafování |
Na mohutnosti kterých množin se ptá zadání úlohy? Na mohutnost množiny vyznačené zeleně \(K \cap H\) (žáci hrající na oba nástroje) a množiny vyznačené modře \(K\) − (\(K \cap H\)) (klavíristé nehrající na housle). Ani u jedné z těchto množin zatím neznáme počet prvků, z toho, co vše již víme, jej však zvládneme vypočítat. Začněme s množinou \(K \cap H\). Víme, že |(\(K \cap H\))'| = 189. Neboli, že z 200 žáků reprezentovaných množinou \(U\) jich 189 spadá do množiny vyznačené šrafováním (\(K \cap H\))'. Zbývajících 11 tak nutně musí spadat do zelené množiny, tedy do množiny \(K \cap H\). Její mohutnost je tedy 11, neboli 11 žáků hraje na oba nástroje.
Zbývá vyřešit, kolik žáků náleží do modré části diagramu. Na to si můžeme sestavit jednoduchou soustavu rovnic. Pro zjednodušení si označme počet prvků (žáků) ve žluté části \(ž\), v modré části pak \(m\). Počet prvků v zelené části již známe, ten je 11. Nyní můžeme sestavit soustavu rovnic:
| \(ž\) + \(m\) + 11 | = | 80 |
| \(ž\) + 11 | = | \(m\) +11+ 13 |
První rovnice říká, že 80 žáků hraje alespoň na jeden z nástrojů (víme ze zadání), druhá pak tvrdí, že počet klavíristů (včetně těch, kteří hrají i na housle) je o 13 vyšší, než počet houslistů (opět včetně těch, kteří hrají na klavír). Je však ve druhé rovnici nutné uvažovat i ty, kteří hrají na oba nástroje? Není, protože kláviristů hrajících na housle je stejně jako houslistů hrajících na klavír. Jsou to přece ti samí žáci. Nebudeme-li tyto žáky uvažovat, zbývajících klavíristů bude stále o 13 víc než zbývajících houslistů. I v případě, že bychom na tuto úvahu nepřišli, jistě bychom si druhou rovnici zjednodušili, protože odečtení jedenáctky od obou jejích stran se přímo nabízí. Zjednodušená soustava tedy vypadá takto:
| \(ž\) + \(m\) + 11 | = | 80 |
| \(ž\) | = | \(m\) + 13 |
Z této soustavy již snad vypočteme, že \(ž\) = 41, a tedy že klavíristů, kteří zároveň nechodí na housle, je 41.
Příklad 3
Autosalon prodává automobily několika značek. Za poslední měsíc bylo prodáno celkem 61 vozů. Automobilů vybavených klimatizací bylo prodáno třikrát více, než automobilů značky Škoda. Automobilů Škoda, které nebyly vybaveny klimatizací, bylo prodáno o 6 méně než škodovek s klimatizací. Aut, která nenesla značku Škoda a zároveň nebyla vybavena klimatizací, bylo prodáno o 3 více, než automobilů Škoda bez klimatizace. Kolik bylo prodáno škodovek? Kolik bylo prodáno klimatizovaných vozů jiné značky než Škoda?
Opět si nejdříve zavedeme několik množin. Za základní množinu \(U\) budeme považovat množinu všech aut prodaných v autosalonu za poslední měsíc. Množina \(Š\) bude množina všech prodaných vozů Škoda, množina \(K\) bude množina všech klimatizovaných vozů. Vennův diagram pro tuto úlohu tak bude velmi podobný těm, které jsme uváděli u předchozích úloh:
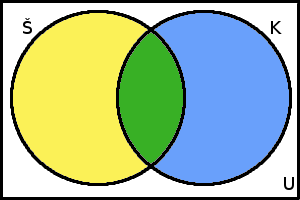
Vennův diagram k Příkladu 3
Již nebudeme rozebírat, jakou množinu reprezentuje která barva, je to obdobné, jako u předchozích úloh. Na rozdíl od nich zde ale známe pouze jedno konkrétní číslo, a to celkový počet prodaných aut, neboli \(|U|\). Ostatní údaje už nám udávají pouze vztahy mezi jednotlivými množinami, nezbývá nic jiného, než začít tvořit soustavu rovnic. Rovnou si tedy zavedeme několik neznámých pro jednotlivé barevné množiny. Proměnná \(ž\) bude značit počet prvků žluté množiny (neklimatizované škodovky), \(z\) zelené (klimatizované škodovky), \(m\) modré (klimatizované vozy jiných značek) a \(b\) bílé (neklimatizované vozy jiných značek) množiny.
Hodnoty kterých neznámých potřebujeme zjistit, abychom úlohu vyřešili? Počet prodaných škodovek je \(ž\) + \(z\), počet prodaných klimatizovaných „neškodovek“ je \(m\). Nyní budeme sestavovat soustavu rovnic, abychom hodnoty těchto neznámých získali.
Budeme postupně do rovnic zapisovat jednotlivé informace ze zadání. První rovnicí můžeme zachytit celkový počet prodaných vozů: \(ž\) + \(z\) + \(m\) + \(b\) = 61. Dále víme, že klimatizovaných vozů bylo prodáno třikrát více než škodovek: \(z\) + \(m\) = 3 (\(ž\) + \(z\)). Další rovnice se týká automobilů Škoda s klimatizací a bez ní: \(ž\) + 6 = \(z\). A zbývá poslední vztah uvedený v zadání: \(b\) = \(ž\) + 3.
Výsledná soustava je:
| \(ž\) + \(z\) + \(m\) + \(b\) | = | 61 |
| \(z\) + \(m\) | = | 3(\(ž\) + \(z\)) |
| \(ž\) + 6 | = | \(z\) |
| \(b\) | = | \(ž\) + 3 |
Nezbývá než tuto soustavu vyřešit, vhodnými úpravami je to velmi rychlé. Zjistíme, že \(ž\) = 5, \(z\) = 11, \(m\) = 37 a \(b\) = 8. Za poslední měsíc bylo tedy prodáno 16 vozů Škoda a 37 klimatizovaných vozů jiných značek.
Podobně mohou být zadány i úlohy vedoucí na větší počet množin, a tedy i na složitější Vennův diagram a složitější soustavu rovnic. U Vennova diagramu pro 3 množiny bychom se tak mohli dostat až k soustavě osmi rovnic o osmi neznámých, která by už pravděpodobně byla poměrně obtížně řešitelná. Pokud však zadání obsahuje konkrétní počty prvků u více částí množin, můžeme se těmto výpočtům vyhnout jako v následující úloze.
Příklad 4
Do třídy 5.A chodí 30 žáků. Hudební školu z této třídy navštěvuje 6 žáků, do modelářského kroužku chodí o 5 žáků více než do hudební školy. Dramatický kroužek navštěvuje o tři žáky méně, než kroužek modelářský. Dva žáci chodí do modelářského kroužku i hudební školy, žádný žák nechodí zároveň do dramatického i modelářského kroužku. 10 žáků nechodí do žádného kroužku. Kolik žáků navštěvuje dvě ze zmíněných zájmových činností?
Základní množinou \(U\) bude množina všech žáků třídy. Dále zavedeme množinu \(H\) žáků chodících do hudební školy, množinu \(M\) žáků navštěvujících modelářský kroužek a množinu \(D\) žáků navštěvujících dramatický kroužek. Vše zaznamenáme do Vennova diagramu pro 3 množiny:
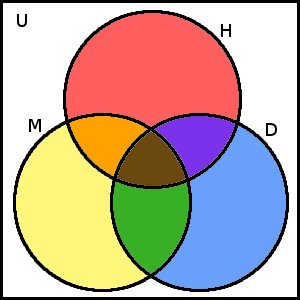
Vennův diagram k Příkladu 4
Opět zavedeme neznámé pro počet prvků množinách vyznačených jednotlivými barvami – \(ž\) pro žlutou, \(m\) pro modrou, \(č\) pro červenou, \(z\) pro zelenou, \(o\) pro oranžovou, \(f\) pro fialovou, \(h\) pro hnědou a \(b\) pro bílou.
U některých těchto neznámých rovnou známe jejich hodnoty. Víme, že \(b\) = 10. Protože žádný žák nenavštěvuje zároveň dramatický a modelářský kroužek, víme také, že \(z\) = 0 a také \(h\) = 0 (nenavštěvuje-li žádný žák dohromady tyto dva kroužky nemůže žádný navštěvovat ani všechny tři zároveň). Dále víme, že \(o\) = 2. Z osmi neznámých nám zbývají čtyři, pro ně již začneme vytvářet rovnice.
Hudební školu navštěvuje 6 žáků, tj. \(č\) + \(o\) + \(h\) + \(f\) = 6. Dosadíme-li již zjištěné hodnoty neznámých, získáme rovnici: \(č\) + 2 + \(f\) = 6, neboli \(č\) + \(f\) = 4. Do modelářského kroužku chodí o 5 žáků více, než do hudební školy, tedy 11. Z toho získáváme \(ž\) + \(o\) + \(h\) + \(z\) = 11. Po dosazení za \(o\), \(h\) a \(z\) dostaneme \(ž\) + 2 = 11. Tím jsme vypočítali další proměnnou, \(ž\) = 9. Dramatický kroužek navštěvuje 8 žáků (11 − 3), rovnice bude \(m\) + \(z\) + \(h\) + \(f\) = 8. Po dosazení za \(z\) a \(h\) dostáváme \(m\) + \(f\) = 8.
Nesmíme také zapomenout na celkový počet studentů. Víme, že celkem je ve třídě 30 studentů, z toho ale 10 nenavštěvuje žádný kroužek. Na kroužky zbývá 20 studentů, tedy \(č\) + \(o\) + \(h\) + \(f\) + \(m\) + \(z\) + \(ž\) = 20. Po dosazení již zjištěných hodnot a úpravě získáme rovnici: \(č\) + \(m\) + \(f\) = 9.
Můžeme zapsat soustavu:
| \(č\) + \(f\) | = | 4 |
| \(m\) + \(f\) | = | 8 |
| \(č\) + \(m\) + \(f\) | = | 9 |
Tuto soustavu snadno dořešíme. K odpovědi na zadání nám navíc z této soustavy stačí znát pouze hodnotu neznámé \(f\), která je 3, dále neznámých \(z\) a \(o\), jejichž hodnoty jsme již určili. Výsledkem je součet těchto neznámých, neboli dvě zájmové činnosti navštěvuje 5 žáků z 5.A.
Na závěr si ukážeme ještě jeden příklad z jiného soudku.
Příklad 5
Zjednodušte následující množinový zápis: [\(C\) \(\cup\) (\(A \cap C\))] \(\cup\) [\(A\) \(\cup\) [\(B\) \(\cap\) (\(A\cup B\))]]
Tento typ úloh můžeme řešit postupnými úpravami podle různých pravidel pro operace s množinami nebo třeba úvahou. My si však ukážeme, jak takovou úlohu vyřešit pomocí Vennova diagramu.
Výsledek tohoto množinového zápisu se budeme snažit zachytit do Vennova diagramu a z něj poté odvodit jednodušší zápis. Budeme postupně zakreslovat jednotlivé operace od nejvnitřnějších závorek. Celý zápis je vlastně sjednocením dvou množin zapsaných opět složitými zápisy. Začněme s levou stranou tohoto sjednocení, tj. s množinou \(C\) \(\cup\) (\(A \cap C\)). Nejdříve zakreslíme průnik množin \(A\) a \(C\) a poté jej sjednotíme s množinou \(C\):
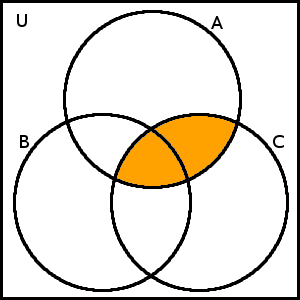
\(A \cap C\)
\(C\) \(\cup\) (\(A \cap C\)) = \(C\)
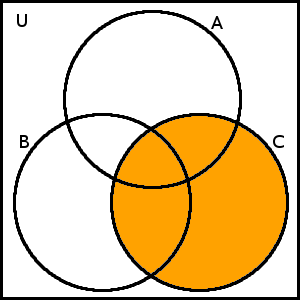
Nyní zakreslíme pravou stranu „nejvyššího“ sjednocení, tedy množinu \(A\) \(\cup\) [\(B\) \(\cap\) (\(A\cup B\))]. Začneme množinou \(A\cup B\), poté provedeme její průnik s množinou \(B\) a následně sjednocení s množinou \(A\):
\(A\cup B\)
\(B\) \(\cap\) (\(A\cup B\))
![A sjednoceno [B průnik (A sjednoceno B)]](obrazky/venn3pr5-3.png)
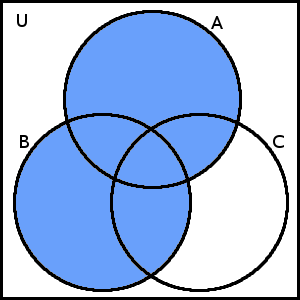
\(A\) \(\cup\) [\(B\) \(\cap\) (\(A\cup B\))] = \(A\cup B\)
Máme zakreslenu levou i pravou stranu „nejvyššího“ sjednocení, nezbývá než toto sjednocení provést:
![[C sjednoceno (A průnik C)] sjednoceno {A sjednoceno [B průnik (A sjednoceno B)]}](obrazky/venn3pr5-5.png)
[\(C\) \(\cup\) (\(A \cap C\))] \(\cup\) [\(A\) \(\cup\) [\(B\) \(\cap\) (\(A\cup B\))]]
Složitý množinový zápis jsme znázornili pomocí Vennova diagramu. Nyní se na diagram podíváme, a zkusíme vymyslet jiný jednodušší zápis, jímž by bylo možné vyznačenou množinu zapsat. V tomto případě to není těžké, jsou vyznačeny všechny tři množiny, neboli v diagramu je zachyceno jejich sjednocení. Zápis ze zadání můžeme tedy zjednodušit na zápis: \(A\) \(\cup\) \(B\cup C\).
U tohoto příkladu si stejně jako u de Morganových vzorců ukažme, že Vennovy diagramy nejsou jediným možným postupem řešení. Podívejme se ještě jednou na zápis [\(C\) \(\cup\) (\(A \cap C\))] \(\cup\) [\(A\) \(\cup\) [\(B\) \(\cap\) (\(A\cup B\))]] a zkusme nad ním chvíli přemýšlet.
Nejprve můžeme zjednodušit např. tuto část: [\(C\) \(\cup\) (\(A \cap C\))]. V množině \(A \cap C\) budou pouze prvky, které mají množiny \(A\) a \(C\) společné. Z toho plyne, že všechny prvky množiny (\(A \cap C\)) jsou zároveň prvky množiny \(C\) (není zde žádný prvek, který by do \(C\) nepatřil). Sjednocením množin \(C\) a (\(A \cap C\)) je tak opět jen množina \(C\), tedy (\(A \cap C\)) = \(C\).
Nyní vezměme druhou část: [\(A\) \(\cup\) [\(B\) \(\cap\) (\(A\cup B\))]]. Podobnou úvahou jako v předchozím případě dojdeme k závěru, že [\(B\) \(\cap\) (\(A\cup B\))] = \(B\) (množina \(A\cup B\) obsahuje totiž všechny prvky množiny \(B\), po průniku s celou množinou \(B\) tak opět získáváme množinu \(B\)). Celý zápis tedy můžeme zjednodušit na \(C\) \(\cup\) (\(A\cup B\)), což lze přepsat jako \(A\) \(\cup\) \(B\cup C\).
