Okolí bodu

Předpokládejme \(a \in \mathbb{R},\, \varepsilon \in \mathbb{R},\, \varepsilon \gt 0\). Označme následujícím způsobem některé intervaly.

Definice

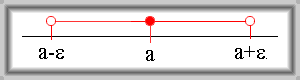
Množinu \(\{x \in \mathbb{R};\, a - \varepsilon \lt x \lt a + \varepsilon\}\) nazýváme okolí bodu \(a\). Číslo \(a\) nazýváme střed okolí, číslo
\(\varepsilon\) nazýváme poloměr okolí.

Značení: \(\mathrm{U}(a,\, \varepsilon)\).

Jiné způsoby zápisu: \((a - \varepsilon,\, a + \varepsilon)\); \(\{x \in \mathbb{R};\, |x - a| \lt \varepsilon\}\)

Pro zdůraznění poloměru okolí se používá též \(\varepsilon\)-okolí bodu \(a\).

Obr. 1.1: Okolí bodu
Hodnota čísla \(\varepsilon\)

\(\varepsilon\) = 2.0
\(\varepsilon\) = 1.5
\(\varepsilon\) = 1.0
\(\varepsilon\) = 0.5
Obr. 1.1: Okolí bodu

Definice

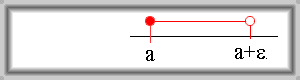
Množinu \(\{x \in \mathbb{R};\, a \leq x \lt a + \varepsilon\}\) nazýváme pravé okolí bodu \(a\).

Značení: \(\mathrm{U}^{+}(a,\, \varepsilon)\).

Jiné způsoby zápisu: \(\langle a,\, a + \varepsilon)\); \(\{x \in \mathbb{R};\, 0 \leq x - a \lt \varepsilon\}\)

Obr. 1.2: Pravé okolí bodu
Hodnota čísla \(\varepsilon\)

\(\varepsilon\) = 2.0
\(\varepsilon\) = 1.5
\(\varepsilon\) = 1.0
\(\varepsilon\) = 0.5
Obr. 1.2: Pravé okolí bodu

Definice

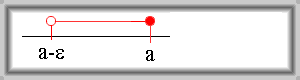
Množinu \(\{x \in \mathbb{R};\, a - \varepsilon \lt x \leq a\}\) nazýváme levé okolí bodu \(a\).

Značení: \(\mathrm{U}^{-}(a,\, \varepsilon)\).

Jiné způsoby zápisu: \((a - \varepsilon,\, a\; \rangle\); \(\{x \in \mathbb{R};\, 0 \leq a - x \lt \varepsilon\}\)

Obr. 1.3: Levé okolí bodu
Hodnota čísla \(\varepsilon\)

\(\varepsilon\) = 2.0
\(\varepsilon\) = 1.5
\(\varepsilon\) = 1.0
\(\varepsilon\) = 0.5
Obr. 1.3: Levé okolí bodu

Definice

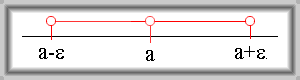
Množinu \(\{x \in \mathbb{R};\, a - \varepsilon \lt x \lt a + \varepsilon \land x \neq a\}\) nazýváme prstencové okolí bodu \(a\).

Značení: \(\mathrm{P}(a,\, \varepsilon)\).

Jiné způsoby zápisu: \((a - \varepsilon,\, a) \cup (a,\, a + \varepsilon)\); \(\{x \in \mathbb{R};\, 0 \lt |x - a| \lt \varepsilon\}\)

Obr. 1.4: Prstencové okolí bodu
Hodnota čísla \(\varepsilon\)

\(\varepsilon\) = 2.0
\(\varepsilon\) = 1.5
\(\varepsilon\) = 1.0
\(\varepsilon\) = 0.5
Obr. 1.4: Prstencové okolí bodu

Definice

Množinu \(\{x \in \mathbb{R};\, a \lt x \lt a + \varepsilon \}\) nazýváme pravé prstencové okolí bodu \(a\).

Značení: \(\mathrm{P}^{+}(a,\, \varepsilon)\).

Jiné způsoby zápisu: \((a,\, a + \varepsilon)\); \(\{x \in \mathbb{R};\, 0 \lt x - a \lt \varepsilon\}\)

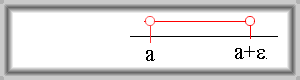
Obr. 1.5: Pravé prstencové okolí bodu
Hodnota čísla \(\varepsilon\)

\(\varepsilon\) = 2.0
\(\varepsilon\) = 1.5
\(\varepsilon\) = 1.0
\(\varepsilon\) = 0.5
Obr. 1.5: Pravé prstencové okolí bodu

Definice

Množinu \(\{x \in \mathbb{R};\, a - \varepsilon \lt x \lt a\}\) nazýváme levé prstencové okolí bodu \(a\).

Značení: \(\mathrm{P}^{-}(a,\, \varepsilon)\).

Jiné způsoby zápisu: \((a - \varepsilon,\, a)\); \(\{x \in \mathbb{R};\, 0 \lt a - x \lt \varepsilon\}\)

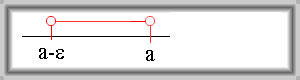
Obr. 1.6: Levé prstencové okolí bodu
Hodnota čísla \(\varepsilon\)

\(\varepsilon\) = 2.0
\(\varepsilon\) = 1.5
\(\varepsilon\) = 1.0
\(\varepsilon\) = 0.5
Obr. 1.6: Levé prstencové okolí bodu

Tabulka shrnující definované pojmy

\(\mathrm{U}(a,\, \varepsilon)\)=\(\{x \in \mathbb{R};\,a - \varepsilon \lt x \lt a + \varepsilon\}\)okolí bodu \(a\)
\(\mathrm{U}^{+}(a,\, \varepsilon)\)=\(\{x \in \mathbb{R};\,a \leq x \lt a + \varepsilon\}\)pravé okolí bodu \(a\)
\(\mathrm{U}^{-}(a,\, \varepsilon)\)=\(\{x \in \mathbb{R};\,a - \varepsilon \lt x \leq a\}\)levé okolí bodu \(a\)
\(\mathrm{P}(a,\, \varepsilon)\)=\(\{x \in \mathbb{R};\,a - \varepsilon \lt x \lt a + \varepsilon \land x \neq a\}\)prstencové okolí bodu \(a\)
\(\mathrm{P}^{+}(a,\, \varepsilon)\)=\(\{x \in \mathbb{R};\,a \lt x \lt a + \varepsilon\}\)pravé prstencové okolí bodu \(a\)
\(\mathrm{P}^{-}(a,\, \varepsilon)\)=\(\{x \in \mathbb{R};\,a - \varepsilon \lt x \lt a\}\)levé prstencové okolí bodu \(a\)