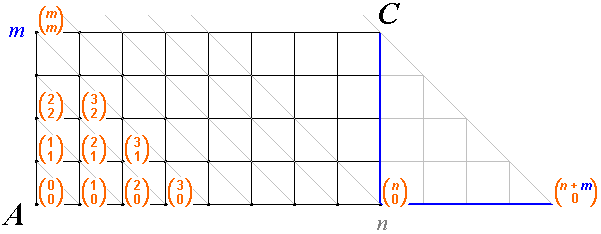
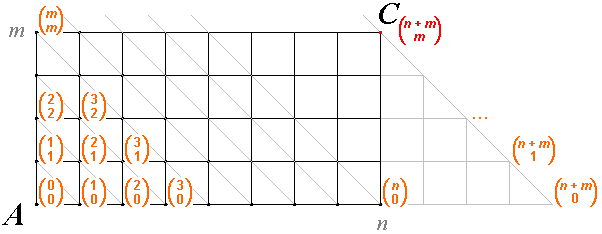
Kombinační čísla

Pascalův trojúhelník

Pascalův trojúhelník je schéma, které dobře znázorňuje některé vlastnosti kombinačních čísel. Můžete se s ním setkat ve dvou tvarech.
(Najetím na prvek v libovolném z obou schémat se v obou schématech barevně označí odpovídající prvek.)

Schéma vlevo zobrazuje základní vztah Pascalova trojúhelníku s kombinačními čísly. Ve schématu vpravo jsou kombinační čísla vyčíslena a dají se v něm lépe vypozorovat některé jejich vlastnosti.

Příklad

Napište osmý řádek Pascalova trojúhelníku.

Řešení

Z předchozího řešení můžeme odvodit, jak obecně vypadá \(n\)-tý řádek Pascalova trojúhelníku:

\(\boldsymbol{n}\)-tý řádek Pascalova trojúhelníku má tvar

Příklad

Napište desátý řádek Pascalova trojúhelníku.

Všimněte si v Pascalově trojúhelníku symetrického rozmístění stejných čísel vzhledem k jeho ose souměrnosti. Je to dané tím, že čísla

která se sobě rovnají, jsou stejně vzdálena od "středu" každého řádku. V následujícím schématu se při najetí myši na některé kombinační číslo barevně označí i číslo, které je ve stejném řádku stejně vzdálené od osy souměrnosti.

Příklad

Dopište druhou polovinu dvanáctého řádku Pascalova trojúhelníku:

\(1 \quad 11 \quad 55 \quad 165 \quad 330 \quad 462 \quad \ldots\)

Řešení

Dvanáctý řádek se skládá ze dvanácti čísel, vypsaných je prvních šest z nich. Protože jsou hodnoty v Pascalově trojúhelníku symetrické podle jeho osy souměrnosti, stačí prvních šest čísel opsat v opačném pořadí. Celý dvanáctý řádek Pascalova trojúhelníku tedy vypadá takto:

\(1 \quad 11 \quad 55 \quad 165 \quad 330 \quad 462 \quad 330 \quad 165 \quad 55 \quad 11 \quad 1\)

Příklad

Dvanáctý řádek Pascalova trojúhelníku má tvar

\(1 \quad 11 \quad 55 \quad 165 \quad 330 \quad 462 \quad 462 \quad 330 \quad 165 \quad 55 \quad 11 \quad 1\).

Odvoďte z něj následující (třináctý) řádek Pascalova trojúhelníku.

Řešení

Na začátku a na konci každého řádku Pascalova trojúhelníku je číslo \(1\). Ostatní čísla odvodíme pomocí vlastnosti

Příklad

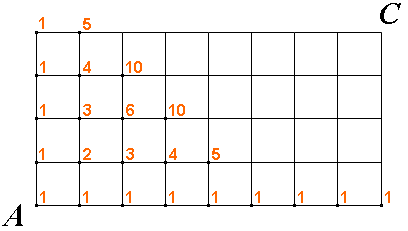
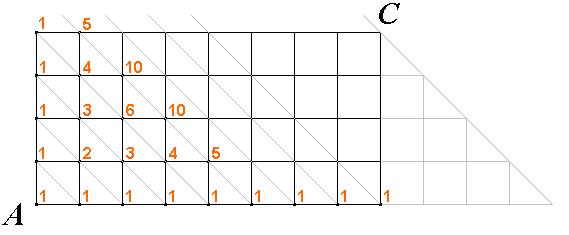
Je dána čtvercová síť, která má \(m \times n\)čtverců. Určete počet nejkratších cest, které vedou v této síti z levého dolního rohu (bod \(A\)) do pravého horního rohu (bod \(C\)).
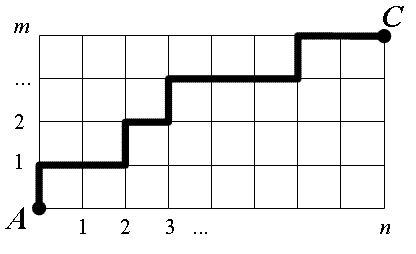
Jedna z takových cest je na obrázku:

Řešení

Nejkratší jsou takové cesty, které se skládají z úseček, po nichž se pohybujeme vpravo nebo nahoru. Na cestě z bodu \(A\) do bodu \(C\)projdeme \(n\) vodorovných a \(m\) svislých úseček, které jsou stranami čtverců sítě. Jestliže délka strany minimálního čtverce sítě je jedna, pak je délka nejkratší cesty \(n+m\). Kolik takových cest je? To je možné spočítat např. následujícími dvěma způsoby.

• Řešení využívající permutace s opakováním

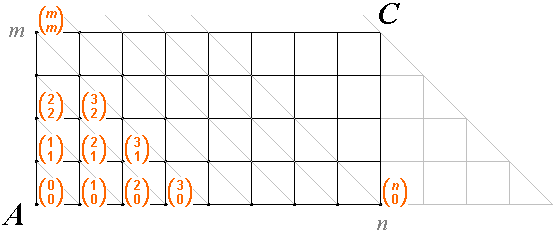
Každé cestě přiřadíme uspořádanou \((n+m)\)-tici složenou z \(n\) nul a \(m\) jedniček, kde nula odpovídá "kroku" doprava a jednička odpovídá "kroku" nahoru. Cestu na obrázku lze tedy zapsat jako uspořádanou \(12\)-tici osmi nul a čtyř jedniček: \((1,0,0,1,0,1,0,0,0,1,0,0)\). Toto přiřazení je vzájemně jednoznačné, takže počet cest z bodu \(A\)do bodu \(C\) je stejný jako počet uspořádaných \((n+m)\)-tic složených z \(n\) nul a \(m\) jedniček. Počet těchto \((n+m)\)-tic je roven \[P'(n,m) = \dfrac{(n+m)!}{n! \cdot m!} = \displaystyle{n+m \choose n} = \displaystyle{n+m \choose m}\] a tolik je také hledaných nejkratších cest z bodu \(A\) do bodu \(C\).

• Řešení využívající znalosti o Pascalově trojúhelníku

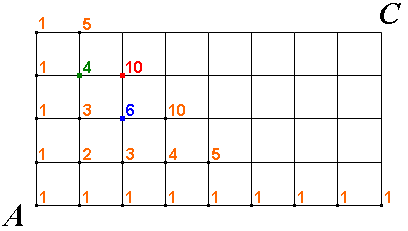
Každému mřížovému bodu přiřadíme číslo, které vyjadřuje počet nejkratších cest z bodu \(A\) do tohoto bodu. Je jasné, že body, do kterých se dá dostat po přímce, budou mít hodnotu \(1\)– nejkratší cesta do nich vede právě po přímce a tedy je jediná.

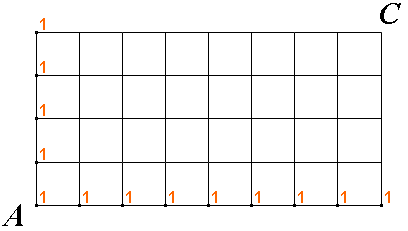
Zkuste sami určit hodnoty v dalších mřížových bodech (začněte nejblíž k bodu \(A\)). Teprve potom si zobrazte pokračování.

Všimněte si podobnosti s Pascalovým trojúhelníkem. Umíte zdůvodnit, že čísla u mřížových bodů skutečně tvoří Pascalův trojúhelník?

Pokud hledáme nejkratší cestu do červeného bodu, dostaneme se do něj pouze ze zeleného bodu (jediným způsobem) nebo z modrého bodu (také jediným způsobem). Pokud tedy do zeleného bodu dojdeme čtyřmi způsoby a do modrého bodu šesti způsoby, pak se do červeného bodu dostaneme \(\color{green}{4} + \color{blue}{6} = \color{red}{10}\) různými způsoby. Podobně to platí pro každý mřížový bod (mimo krajních jedniček). Porovnejte tento závěr s dříve popsanou vlastností Pascalova trojúhelníku.

Dokážete teď určit hodnotu v bodě \(C\)?

Když hodnoty v jednotlivých bodech zapíšeme kombinačními čísly, bude určení hodnoty v bodě \(C\) snadnější.