Základní kombinatorická pravidla

Kombinatorické pravidlo součtu

Také toto pravidlo v životě často využíváme, aniž si to uvědomujeme. Jestliže máme např. tři žluté, dvě modré a čtyři zelené pastelky, umí každý snadno spočítat, že dohromady máme \(3+2+4=9\) pastelek. Matematicky se toto pravidlo formuluje takto:

Příklad

Do třídy chodí \(28\) žáků. Devět z nich jezdí do školy autobusem a tři vozí do školy rodiče autem. Kolik žáků z této třídy chodí do školy pěšky, jestliže nikdo nepoužívá na cestě do školy jiný dopravní prostředek?

Řešení

Počet žáků, kteří jsou z této třídy a chodí do školy pěšky, označíme \(x\). Potom platí:

\(28=9+3+x\)

Vyjádřením \(x\) získáme výsledek:

\(x=28-9-3\)

Z této třídy chodí do školy pěšky \(\boldsymbol{16}\) žáků.

Příklad

V letadle na mezinárodní lince je \(9\) chlapců, \(5\) amerických dětí, \(9\) mužů, \(7\) dětí jiné státní příslušnosti, \(14\) Američanů, z nichž je \(6\) mužů, a \(7\) žen jiné státní příslušnosti. Kolik cestujících je v letadle?

Řešení

Nejprve určíme počet dětí: v letadle je \(5\) amerických dětí a \(7\) dětí jiné státní příslušnosti, to znamená dohromady \(12\) dětí. Dále je v letadle \(7\) žen jiné státní příslušnosti než americké a \(9\) mužů. K určení celkového počtu dospělých tedy zbývá zjistit, kolik amerických žen je v letadle. Ze zadání víme, že je v letadle \(14\) Američanů, z toho \(6\) mužů a \(5\) dětí. Počet amerických žen je proto \(14-6-5=3\). Dostáváme tak počet dospělých: \(9+7+3=19\). V letadle je tedy \(12\) dětí a \(19\) dospělých, což je dohromady \(\boldsymbol{31}\) cestujících. Informace o tom, že v letadle je \(9\) chlapců, není k výpočtu potřeba.

O trochu složitější je určování počtu prvků sjednocení množin v případech, kdy tyto množiny nejsou disjunktní.

Příklad

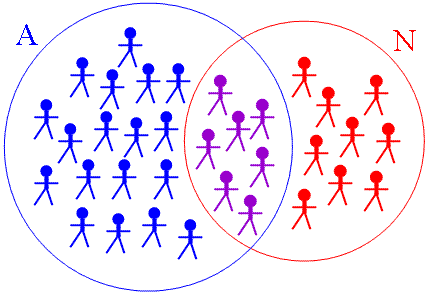
V jedné třídě, ve které každý žák ovládá aspoň jeden ze dvou jazyků (angličtinu nebo němčinu), hovoří \(25\) žáků anglicky, \(16\) žáků německy a \(7\) žáků hovoří oběma jazyky. Kolik žáků chodí do této třídy?

Řešení

Množinu žáků, kteří mluví anglicky, označíme \(A\), a množinu žáků, kteří mluví německy, označíme \(N\). Protože každý žák ve třídě ovládá alespoň jeden z uvedených jazyků, chodí do třídy tolik žáků, kolik prvků má sjednocení množin \(A\) a \(N\). Počet prvků množiny \(X\) označujeme symbolem \(|X|\). Víme, že \(|A|=25\), \(|N|=16\), \(|A \cap N|=7\). Kdybychom jen sečetli \(|A|+|N|\), byli by žáci, kteří mluví oběma jazyky, započítáni dvakrát. Je proto potřeba je jednou odečíst:
\(|A \cup N| = |A| + |N| - |A \cap N| = 25 + 16 - 7 =34\).
Do této třídy chodí \(\boldsymbol{34}\) žáků.

Příklad

Při matematické soutěži řešili žáci tři úlohy; označme je A, B, C. Ze stočtyřiceti soutěžících vyřešilo úlohu A osmdesát, úlohu B sedmdesát a úlohu C padesát soutěžících. Přitom úlohu A a zároveň B vyřešilo čtyřicet soutěžících, úlohu B a zároveň C třicet soutěžících a stejně tak i úlohu A a zároveň C vyřešilo třicet soutěžících. Všechny tři úlohy vyřešilo dvacet soutěžících. Kolik soutěžících nevyřešilo ani jednu úlohu?

Řešení

Budeme postupovat tak, že nejprve zjistíme, kolik žáků vyřešilo alespoň jednu úlohu, a tento mezivýsledek odečteme od celkového počtu soutěžících.
Množinu soutěžících, kteří vyřešili úlohu A (resp. B, C) označíme \(S_A\)(resp. \(S_B\), \(S_C\)). Potom počet soutěžících, kteří vyřešili alespoň jednu úlohu, je stejný, jako počet prvků množiny \(S_A \cup S_B \cup S_C\).

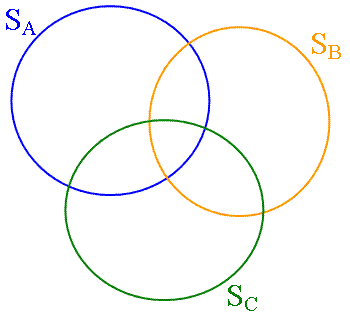
\(|S_A \cup S_B \cup S_C| = |S_A| +|S_B| +|S_C| -|S_A \cap S_B| -|S_A \cap S_C| -|S_B \cap S_C| +|S_A \cap S_B \cap S_C| =\)

\(=80+70+50-40-30-30+20=\)

\(=120\).

Alespoň jednu úlohu vyřešilo \(120\) žáků. Soutěže se zúčastnilo \(140\) žáků, zbývá tedy \(\boldsymbol{20}\) žáků, kteří nevyřešili ani jednu úlohu.