Funkce inverzní
Funkci inverzní určujeme vždy k nějaké původní funkci \(f\). Nutná podmínka pro existenci inverzní funkce je, aby původní funkce \(f\) byla prostá. Původní funkce \(f\) zobrazuje prvky \(D(f)\) na množinu \(H(f)\) a inverzní funkce, kterou značíme \(f^{-1}\), zobrazuje prvky \(H(f)\) na množinu \(D(f)\). Graficky si to lze představit tak, jako bychom k původnímu grafu funkce sestrojili jeho obraz v osové souměrnosti podle osy \(y=x\). Předpis inverzní funkce získáme tak, že se pokusíme vyjádřit \(x\) jako funkci argumentu \(y\).
Definice
Inverzní funkce k prosté funkci \(f\) je funkce \(f^{-1}\), pro kterou platí:
- \(D(f^{-1})=H(f)\) a zároveň
- každému \(y\in D(f^{-1})\) je přiřazeno právě to \(x\in D(f)\), pro které je \(f(x)=y\).
Poznámka
Fakt, že \(D(f^{-1})=H(f)\) se dá snadno převést na poznatek, že \(D(f)=H(f^{-1})\).
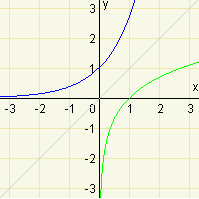
Na obrázku je uveden graf funkce \(f:y=e^x\) (modrou barvou) a k ní funkce inverzní \(f^{-1}:y=\ln x\) (zelenou barvou).
Poznámka
Rozmyslete si, proč je pro existenci inverzní funkce nutná podmínka, aby původní funkce \(f\) byla prostá.

