Definiční obor, obor hodnot
Definiční obor
V definici funkce jsme řekli, že je to předpis na množině \(D\subset\mathbb R\). Máme-li funkci \(f\), pak množině \(D\), na které je tato funkce definována, říkáme definiční obor funkce \(f\) a značíme ji \(D(f)\). Kdybychom použili úvodní analogii s počítačovou klávesnicí, pak to jsou všechny klávesy, kterými je klávesnice vybavena. Mohli bychom také říci, že je to množina všech takových reálných čísel \(x\), pro které nám funkce dá 'rozumné' výsledky.
Příklady
-
Máme dán graf funkce, určete její definiční obor.
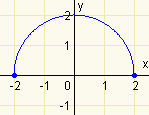
Řešení
Z grafu je vidět, že funkce \(f\) je definována jen pro hodnoty \(x\in\langle -2,2\rangle\) a definiční obor tedy zapíšeme jako \(D(f)=\langle -2,2\rangle\). -
Máme dán předpis funkce \(f(x)={1\over x}\), určete její definiční obor.
Řešení
Jak víme, nulou dělit není možné, a proto \(D(f)=(-\infty,0)\cup(0,+\infty)\). Jinými slovy, funkce je definována pro všechna reálná čísla s výjimkou nuly.
Obor hodnot
Obor hodnot je naopak množina všech reálných čísel \(y\), která dostaneme jako výstupní hodnotu funkce \(f\), jestliže za \(x\) dosadíme všechny přípustné hodnoty z \(D(f)\). Obor hodnot funkce \(f\) značíme \(H(f)\).
Příklady
-
Máme dán předpis funkce \(f:y=x^2\), \(D(f)=\langle -2,2\rangle\). Určete obor hodnot této funkce.
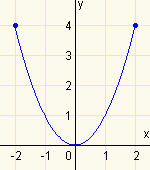
Řešení
Funkční hodnoty pro všechna \(x\in\langle -2,2\rangle\) nabývají pouze nezáporných hodnot menších nebo rovných 4, obor hodnot zapíšeme jako \(H(f)=\langle 0,4\rangle\). -
Máme dán předpis funkce \(f:y=x\). Určete obor hodnot pro tuto funkci.
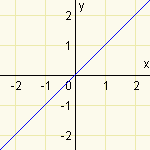
Řešení
Funkční hodnoty pro všechna \(x\in D(f)\) nabývají hodnot všech reálných čísel, obor hodnot zapíšeme jako \(H(f)=\mathbb R\).
