Sylabus - Kuželosečky
Definice kuželoseček, ohniskové vlastnosti kuželoseček, společná poměrová definice všech kuželoseček, kuželosečky jako řezy kuželových ploch, Quetelet-Dandelinovy věty. Konstrukce tečen kuželoseček, konstrukce středů oskulačních kružnic. Bodová, zahradnická, trojúhelníková, proužková (součtová, rozdílová), příčková, Rytzova konstrukce elipsy. Parabola - subnormála, subtangenta, bodová a lichoběžníková konstrukce. Hyperbola - bodová konstrukce, věty o sečnách a tečnách hyperboly, konstrukce velikosti hlavní a vedlejší poloosy, známe-li asymptoty hyperboly a jeden její bod. Využití osové afinity a perspektivní kolineace při konstrukci kuželoseček.
K tomuto tématu vznikla velice pěkná diplomová práce Věry Effenberger Využití internetu při výuce kuželoseček na středních školách. Tato práce svým obsahem výrazně převyšuje středoškolskou látku a doporučuji ji jako studijní materiál i pro studenty vysokých škol. Není tedy účelem přepsat zde obsah této práze, zaměřím se pouze na témata, která v diplomové práci nejsou zastoupena, či nejsou zpracována dostatečně pro účel předmětu Deskriptivní geometrie I.
Úvod
Kuželosečky jsou křivky, které, jak nám napovídá jejich název, lze vytvořit jako řezy rotační kuželové plochy rovinou. S takto vytvořenými křivkami se denně setkáváme v běžném životě. Představte si například hranici hladiny vody v nakloněné sklenici, tužku ve tvaru šestibokého hranolu ořezanou pomocí ořezávátka, či obyčejnou seříznutou šišku salámu. Při nepatrné dávce fantazie můžeme ve všech těchto předmětech vidět kuželosečky. Snadno si totiž představíme, že sklenice, či ořezaná část tužky tvoří kuželovou plochu (u salámu se jedná o plochu válcovou) a hladina vody, popřípadě jedna stěna tužky představuje rovinu řezu.
To vše je jen nepatrný zlomek situací, v nichž se můžeme setkat s kuželosečkami. Tyto křivky mají též široké uplatnění v architektuře, plochy od nich odvozené se používají v radiotechnice, astronomii a v řadě dalších oblastí.
Společná definice
Definice elipsy a hyperboly se na první pohled liší od definice paraboly. Všechny tři kuželosečky lze definovat následovně jednotným způsobem.
Kuželosečky jsou množiny všech bodů v rovině, které mají od pevného bodu F a pevně zvolené přímky d, neprocházející bodem F, stálý poměr vzdáleností rovný konstantě k. Je-li k < 1 je touto kuželosečkou elipsa, pro k = 1 dostáváme parabolu a pro k > 1 dostáváme hyperbolu.Bod F se nazývá ohniskem kuželosečky, přímka d řídící přímkou (direktrix). Číslo k se nazývá numerická výstřednost. Tímto způsobem můžeme definovat všechny regulární kuželosečky vyjma kružnice.
|
Zde si můžete applet stáhnout do svého počítače.
|
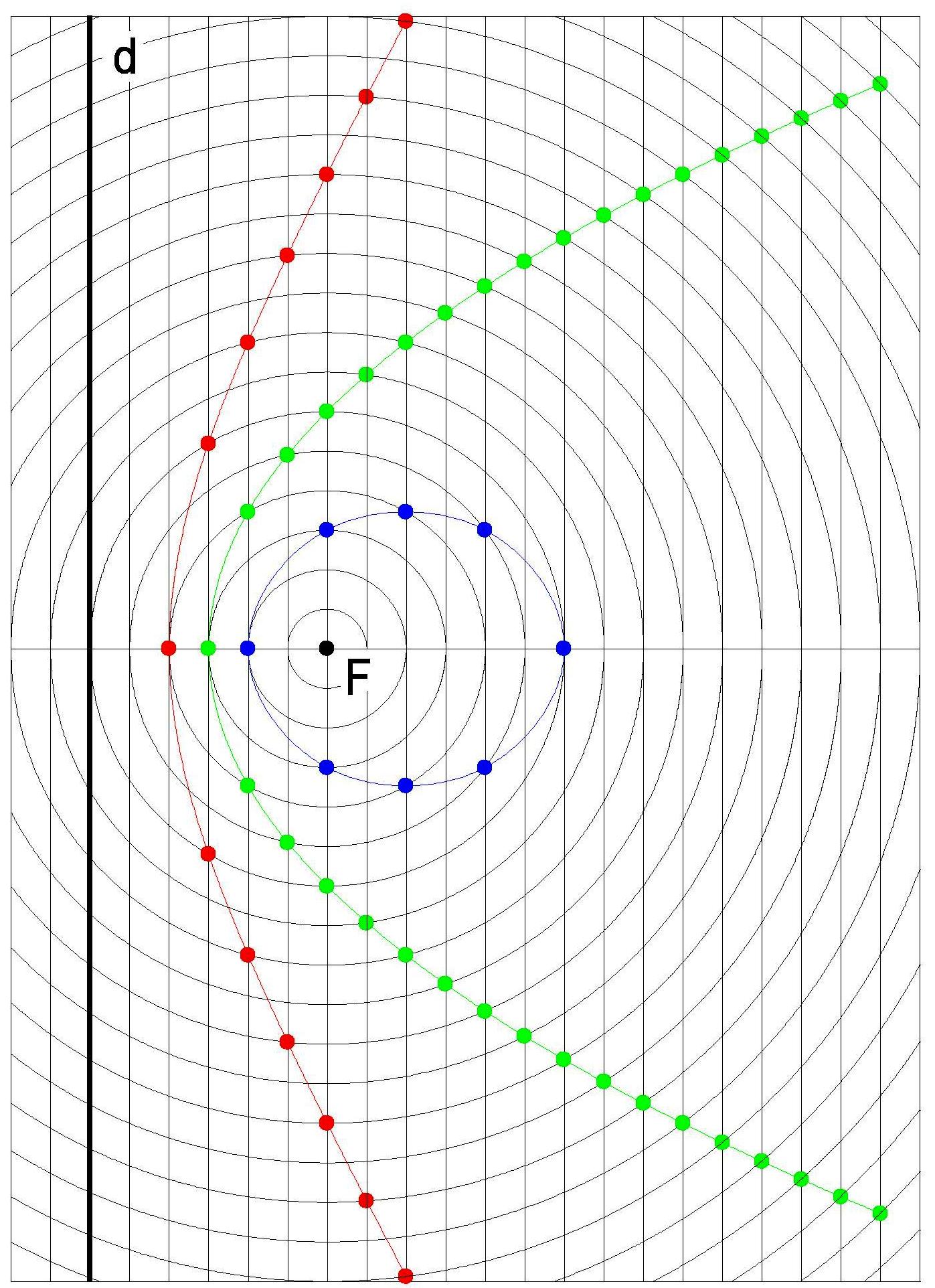Pro demonstraci konstrukce kuželoseček na základě společné poměrové definice lze na střední škole s výhodou využít vhodné sítě kružnic a přímek. Ukázka takové sítě včetně zakreslených kuželoseček je znázorněna na obrázku vpravo. Jedná se o soustavu soustředných kružnic, jejichž poloměry se liší o zvolenou jednotku a soustavu rovnoběžných přímek, jejichž vzdálenost je rovna téže jednotce a jedna z přímek prochází středem soustavy kružnic. Zvolíme-li ohnisko F ve středu soustavy kružnic a řídicí přímku ztotžníme s libovolnou přímkou ze soustavy přímek (tak, aby F ∉ d), můžeme jednotlivé body kuželoseček hledat jako průsečíky kružnic a přímek jejichž poloměr a vzdálenost od řídicí přímky jsou ve zvoleném poměru.
Na obrázcích dole je znázorněna síť vhodná ke konstrukci bodů elipsy a hyperboly na základě jejich součtové, resp. rozdílové definice. Tato síť je tvořena dvěma soustavami soustředných kružnic, jejichž poloměry se liší o zvolenou jednotku (stejnou pro obě soustavy). Zvolíme-li ohniska ve středech obou soustav kružnic, můžeme konstruovat body elipsy (hyperboly) jako průsečíky kružnic, jejichž součet (absolutní hodnota rozdílu) poloměrů je roven zvolené hodnotě 2a. Oba typy sítí je možné stáhnout zde.
Konstrukce hyperboly
Představme si konstrukci hyperboly, kterou budeme využívat např. při hledání obrazu hyperboly v různých zobrazovacích metodách. Při promítání hyperboly se často nezachovávají osy, vrcholy či ohniska (míněno tak, že průmět osy hyperboly nemusí být osou průmětu hyperboly). Zato se zachovávají tečny hyperboly a tedy i asymptoty. K jednoznačnému zadání hyperboly stačí znát její asymptoty a jeden její bod.
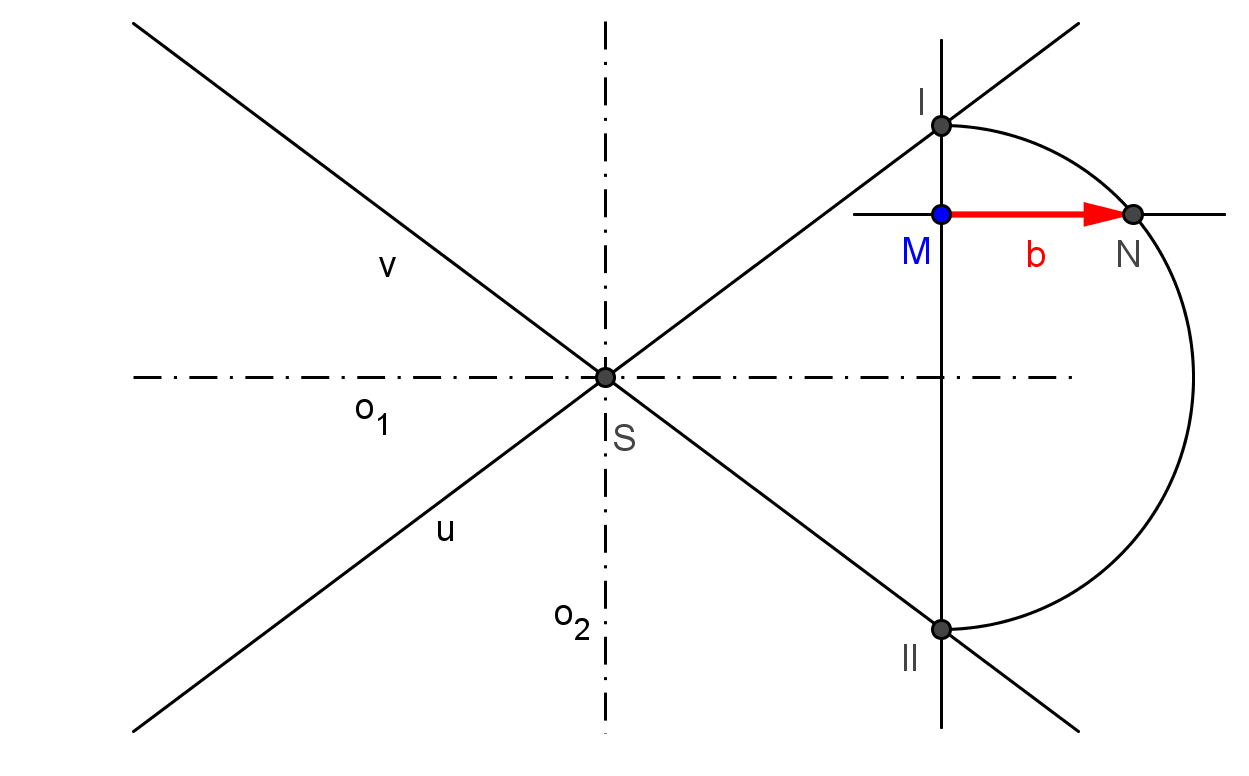Uvažujme hyperbolu zadanou asymptotami u, v a jedním bodem M (M ∉ u, v). Osy hyperboly jsou symetrálami úhlů, které svírají asymptoty u, v. Chceme-li získat velikost vedlejší poloosy hledané hyperboly, vedeme bodem M rovnoběžku s vedlejší osou o2. Její průsečíky s asymptotami označme I, II. Sestrojme nad průměrem I II půlkružnici a bodem M veďme přímku rovnoběžnou s hlavní osou hyperboly. Tato přímka protne půlkružnici v bodě N, pro nějž platí, že |MN| = b.
Tato konstrukce je zobrazena i v následujícím appletu. Můžete zde měnit polohu bodů M a F. Při změně polohy bodu M si všimněte, že se mění vzdálenost bodů I, II, ale vzdálenost bodů M, N zůstává stálá. Změnou polohy ohniska získáte jinou hyperbolu, na níž si opět můžete vyzkoušet správnost konstrukce.
|
Zde si můžete applet stáhnout do svého počítače.
|
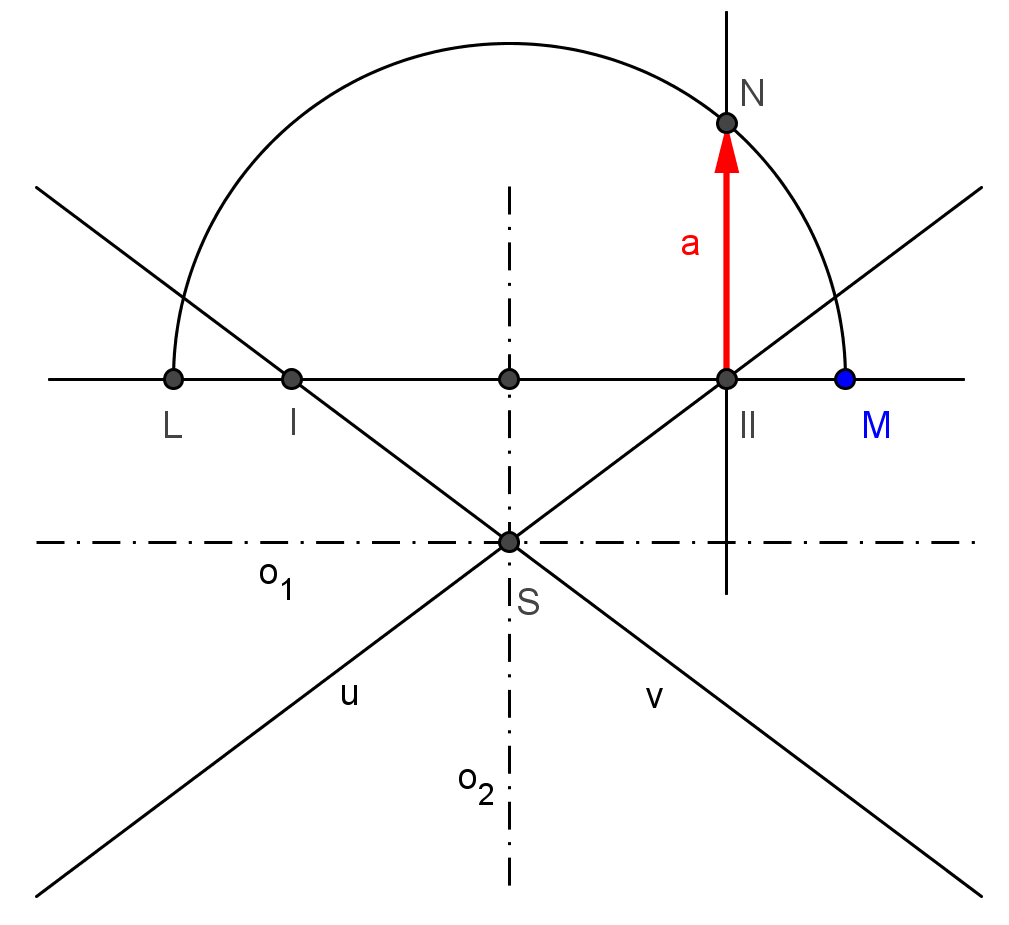
Obdobně můžeme zkonstruovat i velikost hlavní poloosy a. Veďme tentokrát bodem M rovnoběžku s hlavní osou o1. Její průsečíky s asymptotami označme opět I, II. Na přímce I II sestrojme bod L souměrně sdružený s bodem M podle vedlejší osy. Sestrojme nad průměrem LM půlkružnici a např. bodem II veďme přímku rovnoběžnou s vedlejší osou hyperboly. Tato přímka protne půlkružnici v bodě N, pro nějž platí, že |IIN| = a.
Tato konstrukce je zobrazena i v následujícím appletu. Můžete zde měnit polohu bodů M a F. Při změně polohy bodu M si všimněte, že se mění vzdálenost bodů M, L, ale vzdálenost bodů II, N zůstává stálá. Změnou polohy ohniska získáte jinou hyperbolu, na níž si opět můžete vyzkoušet správnost konstrukce.
|
Zde si můžete applet stáhnout do svého počítače.
|
Odvození konstrukce velikosti vedlejší poloosy:
Při odvozování správnosti této konstrukce je třeba si uvědomit následující:
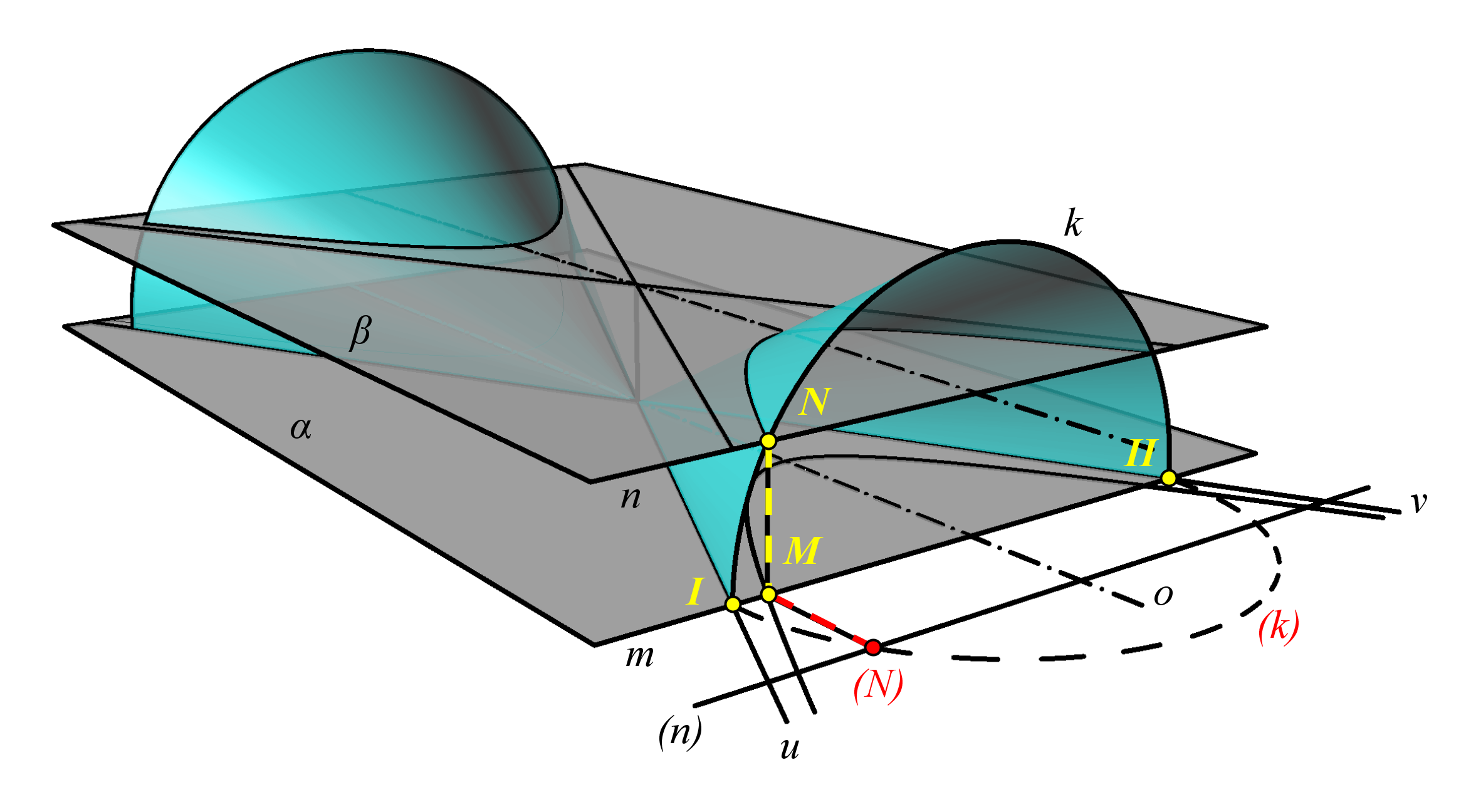
Uvažujme kuželovou plochu, jejíž površky svírají s osou kuželové plochy úhel φ. Dále uvažujme rovinu α, která prochází osou a protíná kuželovou plochu ve dvou povrchových přímkách p, q (v následujících obrázcích je zobrazena vždy jen část plochy „nad“ rovinou α). Každá rovina β, rovnoběžná s rovinou α (α ∉ β) protíná kuželovou plochu v hyperbole, jejíž asymptoty jsou rovnoběžné s povrchovými přímkami p, g (jsou to jediné přímky kuželové plochy, které rovina β neprotíná ve vlastních bodech, určují tedy směry asymptot hyperboly).
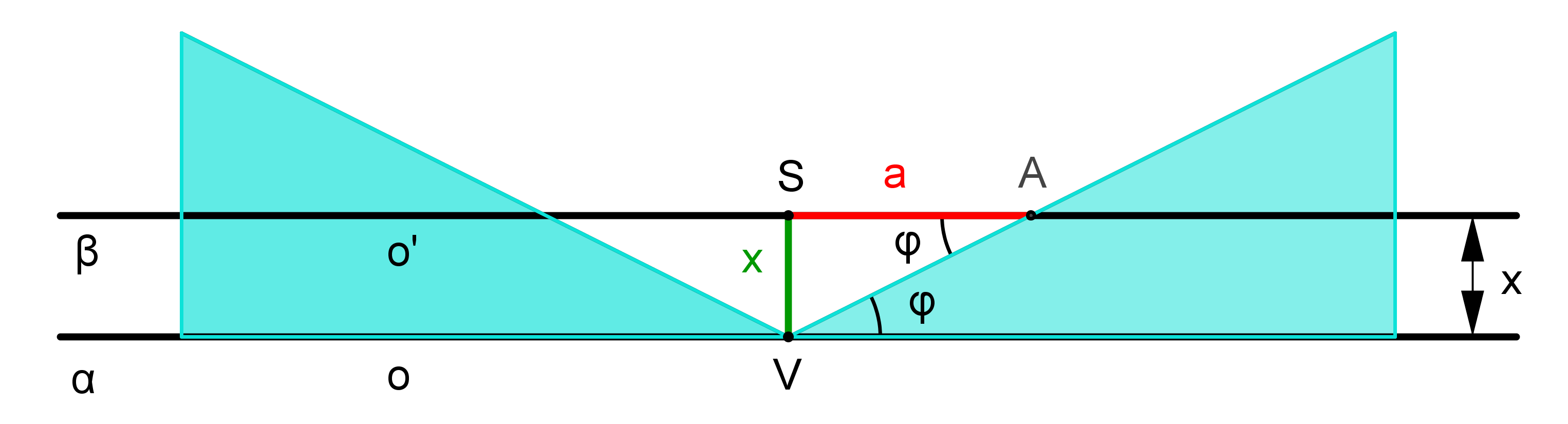
Dále platí, že vzdálenost rovin α a β je stejná, jako velikost vedlejší poloosy hyperboly řezu, ležící v rovině β. V následujícím obrázku je znázorněn řez rovinou, která obsahuje osu o kuželové plochy a je kolmá k rovině α. V této rovině leží i hlavní osa hyperboly řezu o’. Označme V vrchol kuželové plochy, S střed hyperboly řezu a A jeden její vrchol. Vzdálenost |VS|, tj. vzdálenost rovin α, β označme x. Površka VA kuželové plochy svírá s osou o kuželové plochy a tedy i s hlavní osou o’ hyperboly úhel φ. Označme dále a velikost hlavní poloosy hyperboly a = |SA|. V pravoúhlém trojúhelníku VAS platí tg φ = x/a. Asymptoty hyperboly svírají s hlavní osou hyperboly rovněž úhel φ, stejný vztah (tg φ = b/a) tedy platí i pro velikost b vedlejší poloosy hyperboly řezu, tj. b = x.
Vraťme se k naší konstrukci. Hyperbola je dána asymptotami u, v a jedním bodem M. Představme si kuželovou plochu, která protíná rovinu papíru (α) právě ve zvolených asymptotách. Bod M nechť je pravoúhlý průmět (do roviny α) bodu N kuželové plochy, který leží v rovině řezu (β), jejíž vzdálenost od průmětny je rovna velikosti vedlejší poloosy hyperboly řezu. Uvažujme řez třetí rovinou γ, procházející bodem M kolmo k ose kuželové plochy. Tato rovina protne kuželovou plochu v kružnici k, roviny α a β protne ve dvou rovnoběžných přímkách m, n, přičemž M ∈ m, N ∈ n. Rovinu γ sklopíme do roviny α. Velikost vedlejší poloosy je rovna vzdálenosti (M)(N), kde (M) = M, (N) ∈ (k) a zároveň úsečka M(N) je kolmá na m.
Lichoběžníková konstrukce paraboly
Stejně jako u předchozí konstrukce hyperboly, i konstrukce popsané v následujících řádcích budeme často využívat při zobrazování paraboly v osové afinitě nebo pomocí libovolné zobrazovací metody, kdy se většinou nezachová osa, ohnisko, či vrchol paraboly, ale není problém najít obraz libovolného bodu paraboly a obraz tečny v daném bodě. Najdeme-li dva takové body i s tečnami, můžeme parabolu sestrojit.
Věta: Spojnice průsečíku dvou různých tečen paraboly se středem tětivy určené jejich dotykovými body je rovnoběžná s osou paraboly.
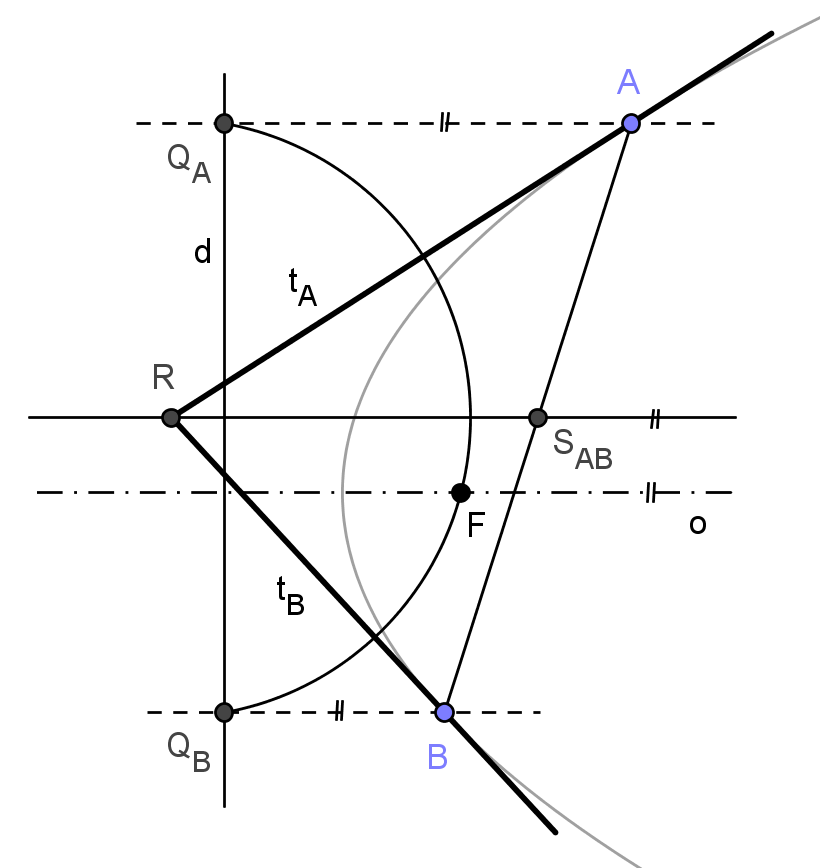
Důkaz: Uvažujme na parabole tečny tA, tB s body dotyku A, B. Střed tětivy A, B, paraboly označme SAB, průsečík tečen tA, tB označme R. Dokážeme, že přímka SABR je rovnoběžná s osou paraboly.
Označme dále QA, QB paty kolmic vedených z bodů A, B na řídicí přímku paraboly d.
Víme, že tečna paraboly půlí vnější úhel průvodičů (ten, mezi jehož rameny leží vrchol paraboly). Všechny body Q souměrně sdružené s ohniskem podle tečny paraboly leží na řídicí přímce d. Pro každý bod X tečny paraboly a příslušný bod Q tedy platí |XF| = |XQ|. Tedy i pro průsečík R tečen tA, tB musí platit |RQA| = |RF| = |RQB|. Body R i SAB leží na ose pásu určeného přímkami AQA a BQB, platí tedy RSAB || o. ■
Vlastnost popsaná v předchozí větě je demonstrována v následujícím appletu, v němž můžete měnit polohu bodu B.
|
Zde si můžete applet stáhnout do svého počítače.
|
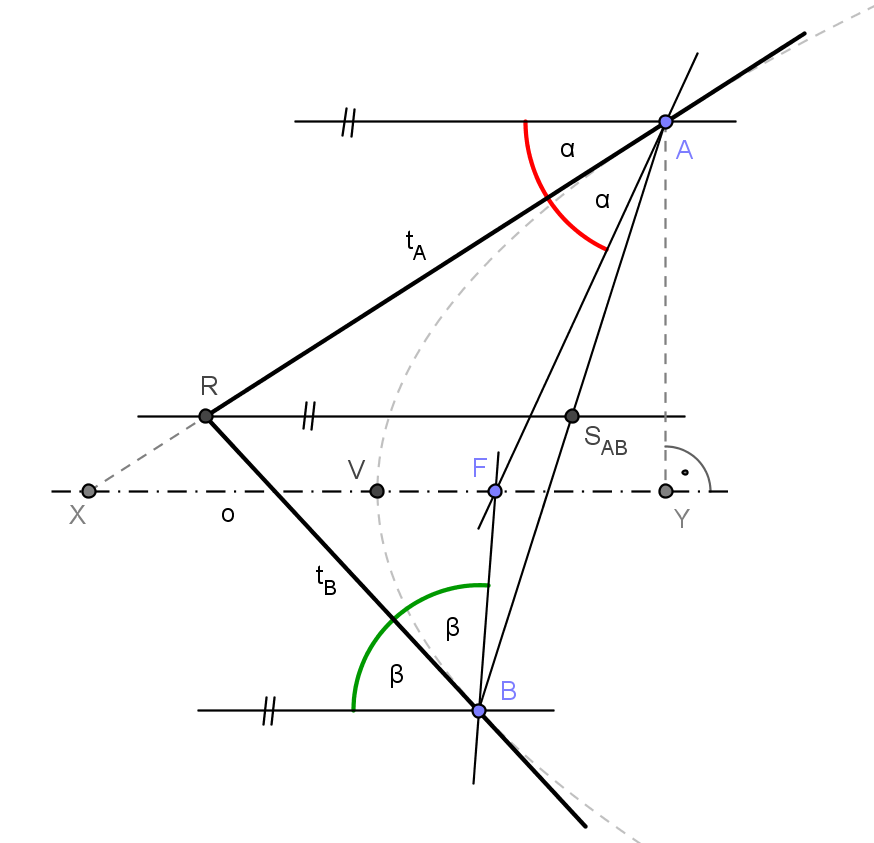
Uvažujme nyní parabolu zadanou dvěma tečnami tA, tB s body dotyku A, B. Pomocí předchozí věty získáme směr osy paraboly. Osu, vrchol či ohnisko paraboly můžeme sestrojit více způsoby. Například můžeme využít toho, že osa půlí úhel průvodičů (levý obrázek). Přímky, na nichž leží průvodiče rovnoběžné s osou paraboly (AQA, BQB), umíme sestrojit, snadno tedy sestrojíme i přímky, na nichž leží průvodiče AF a BF jako obrazy AQA resp. BQB v osové souměrnosti podle tečen tA resp. tB. Průsečíkem těchto přímek je ohnisko paraboly F. Osa paraboly prochází ohniskem a je rovnoběžná s RSAB. Vrchol můžeme dourčit např. jako střed úsečky XY, kde X je průsečík tečny tA s osou o a Y je pata kolmice spuštěné z bodu A na osu (XY - subtangenta)
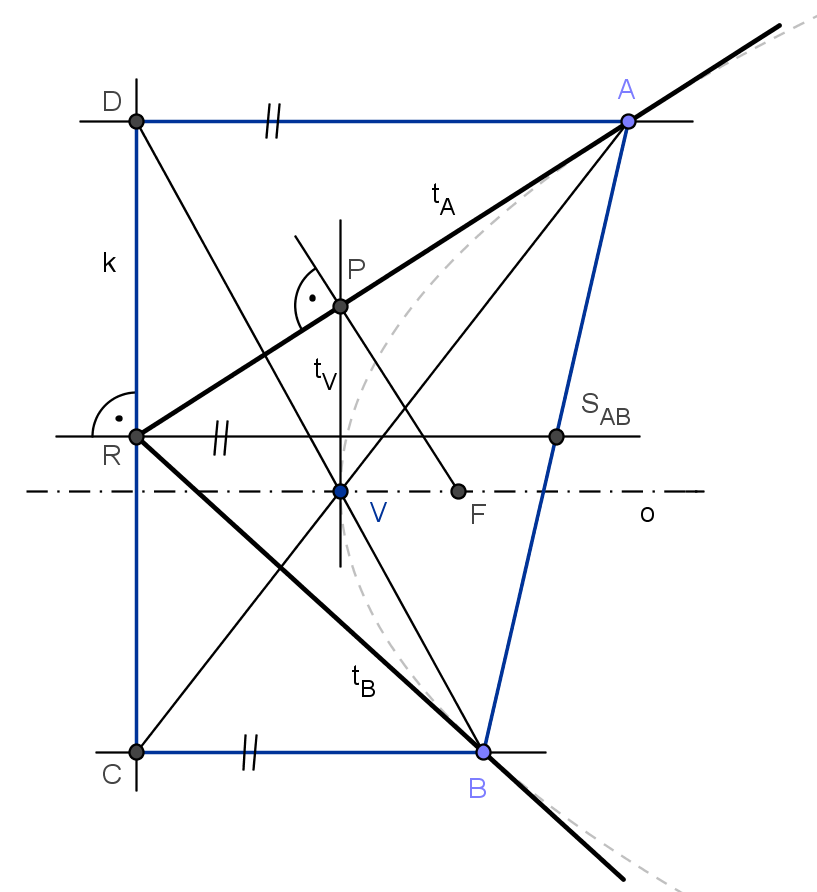
Další možností je využití tzv. lichoběžníkové konstrukce (pravý obrázek), při níž sestrojíme přímo vrchol paraboly V. Veďme nyní bodem R kolmici k ke směru osy paraboly. Body A, B veďme rovnoběžky s osou, jejich průsečíky s kolmicí k označme C, D. Vrchol V paraboly sestrojíme jako průsečík přímek AC a BD. Osa paraboly prochází vrcholem a je rovnoběžná s RSAB. Ke konstrukci ohniska můžeme využít např. vrcholovou tečnu (V ∈ tV, tV ⊥ o), na níž leží paty všech kolmic spuštěných z ohniska na tečny paraboly.
Body A, B, C, D (ne nutně v tomto pořadí) jsou vrcholy lichoběžníku (není-li spojnice AB kolmá k ose paraboly), podle nějž dostala tato konstrukce svůj název. Leží-li body A, B v opačných polorovinách určených osou o, je vrchol průsečíkem úhlopříček tohoto lichoběžníku, leží-li v téže polorovině, je vrchol V průsečíkem jeho ramen.