Sylabus - Osová afinita a středová kolineace
1) Nevlastní elementy, klasifikace kolineací.
2) Osová afinita – osová afinita mezi dvěma rovinami, osová afinita v rovině, osa afinity, směr afinity, charakteristika osové afinity, obraz kružnice v osové afinitě, využití osové afinity při řezech těles.
3) Středová kolineace – mezi dvěma rovinami, střed, osa, úběžnicové roviny kolineace; invarianty středového promítání; středová kolineace v rovině, střed, osa, úběžnice kolineace, obraz kružnice ve středové kolineaci, využití středové kolineace při řezech těles.
K tomuto tématu vznikla pěkná diplomová práce Petry Plichtové Webová aplikace pro výuku osové afinity a středové kolineace. Tato práce je určena pro středoškolské studenty, ale řada partií je plně využitelná i pro vysokoškolské studenty. V následujícím textu se na ni budu často odkazovat.
Klasifikace kolineací
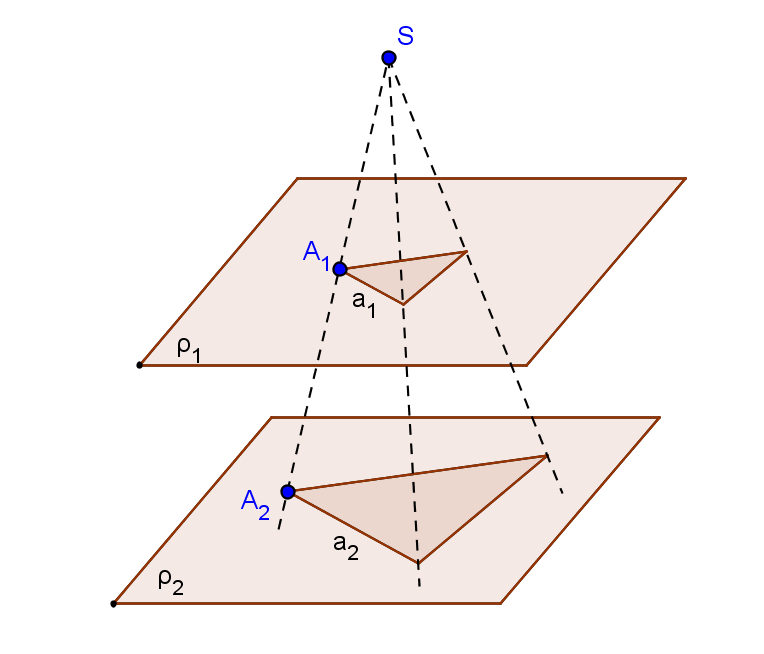
Uvažujme v rozšířeném euklidovském prostoru dvě roviny ρ1 a ρ2 a bod S, který neleží v žádné z nich. Definujme následující promítání (viz [6], str. 102):
Nechť jsou dány roviny ρ1, ρ2 a bod S, který není s nimi incidentní. Příbuznost mezi oběma rovinami, v níž bodu jedné roviny odpovídá jeho průmět ze středu S do druhé roviny, se nazývá kolineace mezi dvěma rovinami ρ1, ρ2 (zprostředkovaná středem promítání S).
Toto promítání je vzájemně jednoznačné. Každému bodu roviny ρ1 odpovídá právě jeden bod roviny ρ2 a naopak. Obrazem bodu je tedy bod, obrazem přímky je přímka, bodu na přímce odpovídá opět bod na přímce.
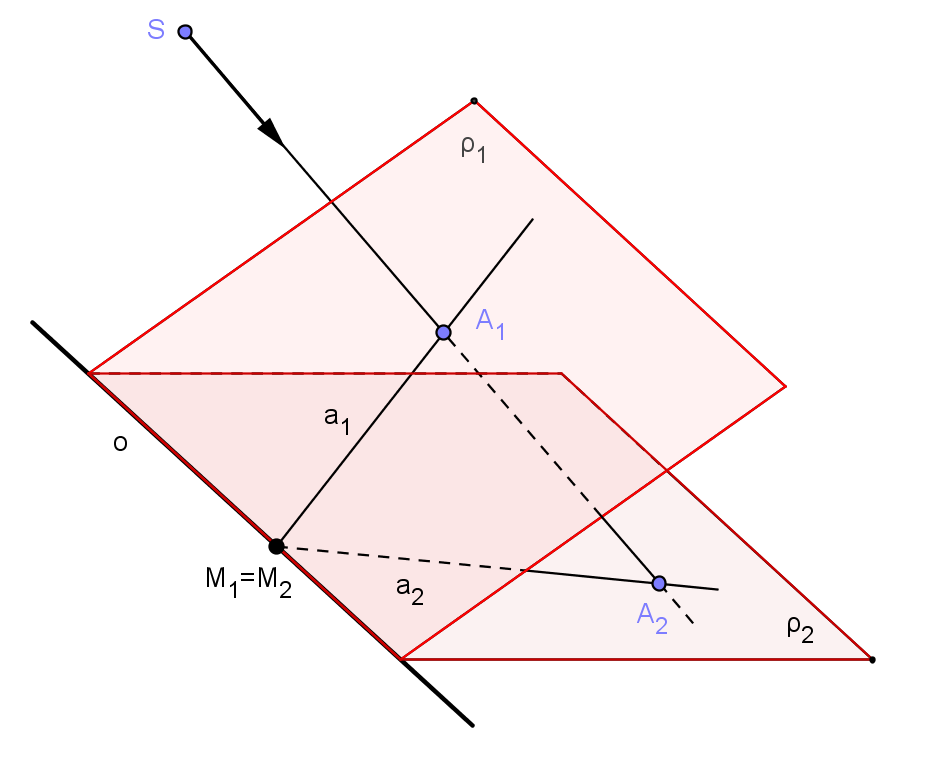
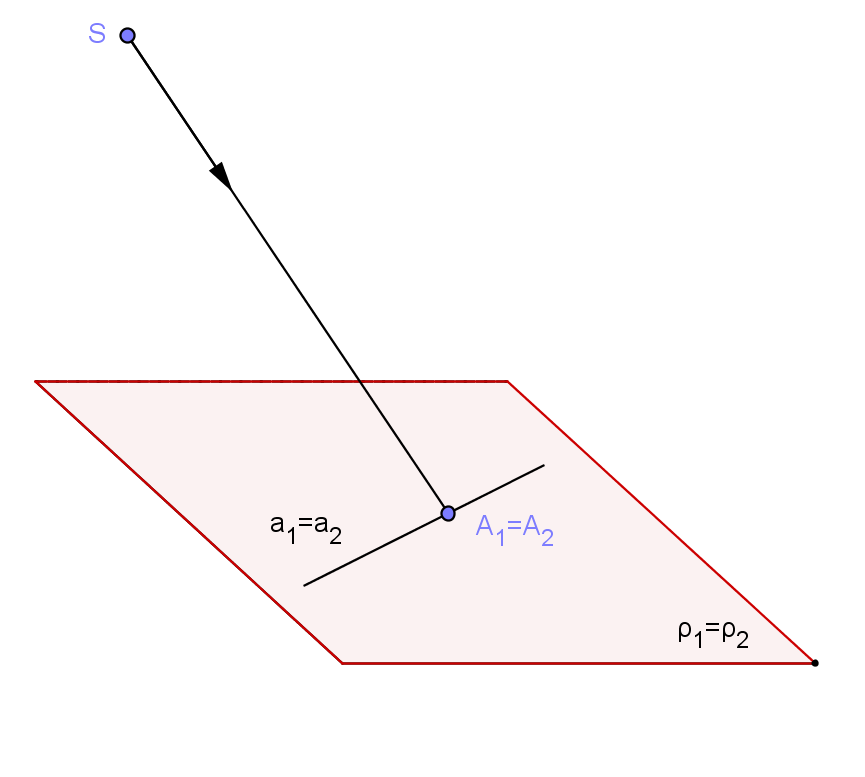
Střed promítání S nazýváme středem kolineace. Jsou-li roviny ρ1, ρ2 různé (viz levý obrázek), pak jejich průsečnici o nazýváme osou kolineace. Pro každý bod na ose kolineace platí M1 = M2 a je tedy samodružným bodem kolineace. Body mimo osu tuto vlastnost nemají a tedy neexistují žádné další samodružné body. Jestliže roviny ρ1, ρ2 splývají (viz pravý obrázek), pak je každý bod samodružný a kolineace je identitou.
Věta: Nesamodružné přímky, které si odpovídají v neidentické kolineaci se protínají na ose kolineace.
Důkaz věty viz např. [6], str. 103)
Budeme-li rozlišovat vlastní a nevlastní body, dostaneme několik příbuzností, které jsou speciálními případy kolineace mezi dvěma rovinami. Střed i osa kolineace mohou být vlastní nebo nevlastní. Je-li osa kolineace nevlastní, jsou roviny ρ1, ρ2 vzájemně rovnoběžné. Je-li navíc střed kolineace nevlastním bodem, dostáváme posunutí roviny ρ1 do roviny ρ2 (viz obr. 1, obrázky vytvořeny podle [6]). Pro vlastní střed a nevlastní osu dostáváme stejnolehlost mezi rovinami ρ1, ρ2 (viz obr. 2).
Je-li osa kolineace vlastní přímka, pak pro vlastní střed dostáváme středovou kolineaci mezi dvěma rovinami (viz obr. 3) a pro nevlastní střed dostáváme osovou afinitu mezi dvěma rovinami (viz obr. 4). Osová afinita zachovává vlastní a nevlastní prvky, zatímco ve středové kolineaci může vlastnímu bodu (přímce) jedné roviny odpovídat nevlastní bod (přímka) druhé roviny. Takový bod (přímku) nazýváme úběžníkem (úběžnicí) první roviny.
1)2)
3)
4) 
Osová afinita mezi dvěma rovinami
| Ke stažení: pracovní listy používané při přednáškách, příklady na procvičení látky |
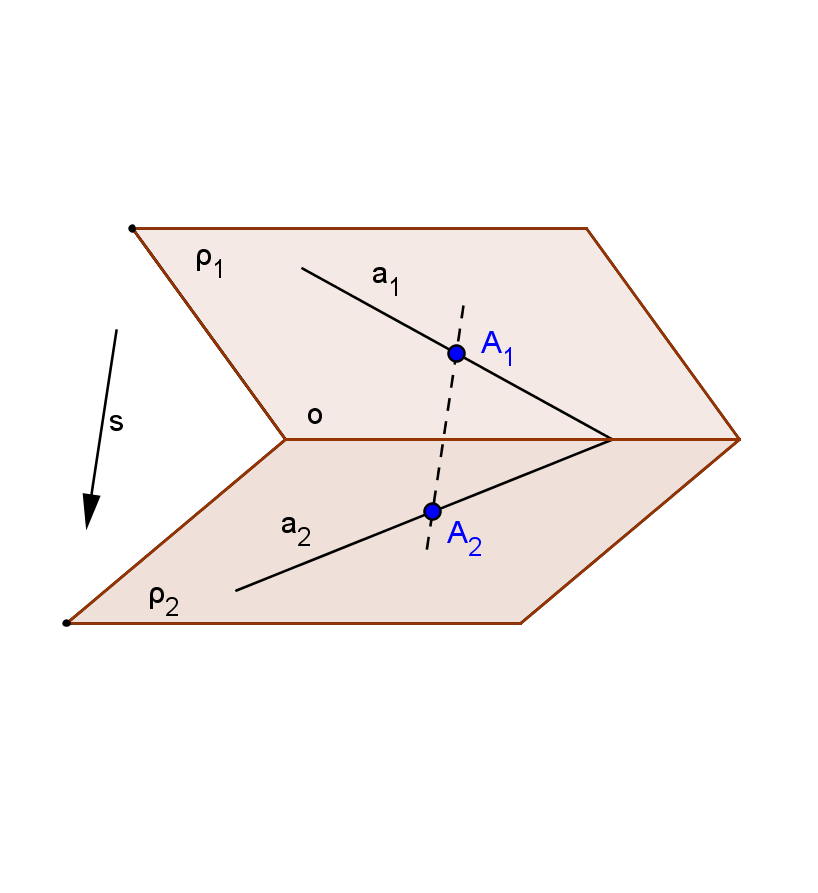
Je-li střed kolineace mezi dvěma různoběžnými rovinami nevlastním bodem ve směru s, který není rovnoběžný se žádnou se zvolených rovin, nazývá se příbuznost, kterou získáme tímto rovnoběžným promítáním, perspektivní či osovou afinitou mezi dvěma rovinami.
Směr s je směrem afinity.
Průsečnice o obou rovin je osou afinity.
Osová afinita je určena, jsou-li dány roviny ρ1, ρ2 a směr s.
Věta: Dvojice afinně sdružených bodů leží na přímkách rovnoběžných se směrem afinity.
Věta: Afinně sdružené přímky se protínají na ose afinity.
Věta: Nevlastní přímka jedné roviny přechází afinní transformací do nevlastní přímky druhé roviny.
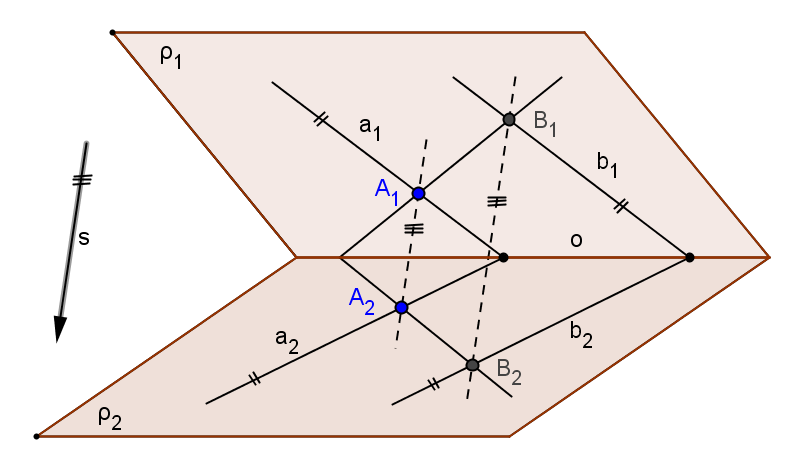
Osová afinita mezi dvěma rovinami je určena, jsou-li dány:
• Osa afinity a dvojice sdružených bodů
• Osa afinity a dvojice sdružených přímek protínajících se na ose o a směr afinity ležící v rovině určené touto dvojicí
• Tři dvojice sdružených bodů takových, že jejich spojnice jsou navzájem rovnoběžné
• Dvojice sdružených bodů, jejichž spojnice bude rovnoběžná s rovinou protínající se dvojice sdružených přímek
Věta: Osová afinita zachovává dělicí poměr.
Složení dvou afinit se společnou osou
Uvažujme tři roviny α, α' a α'', které se protínají v přímce o. Složením osové afinity mezi rovinami α, α' (A → A') a osové afinity mezi rovinami α', α'' (A' → A'') dostáváme opět osovou afinitu, zobrazující body roviny α do roviny α'' (A → A'').
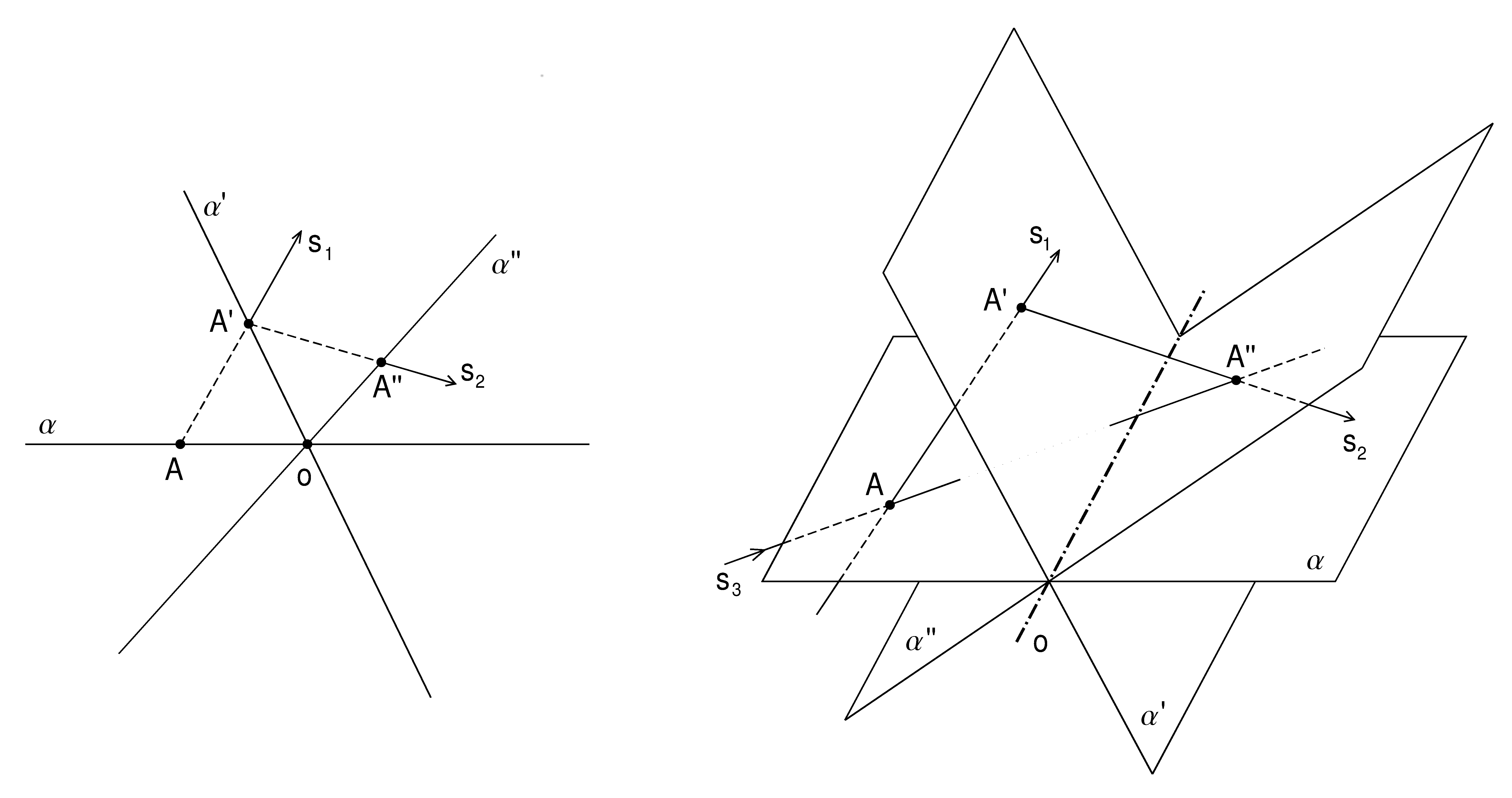
Splyne-li α'' s α, dostáváme rovinné zobrazení - osovou afinitu v rovině. Skládáním osových afinit se společnou osou můžeme získat i identitu. Na následujícím obrázku vpravo je naznačeno užití skládání afinit při otáčení roviny α do průmětny π (A → A1, A → Ao, A1 → Ao).
Osová afinita v rovině
O pár řádků výše jsme si ukázali jeden z možných způsobů, jak získat osovou afinitu v rovině a to pomocí skládání osových afinit mezi dvěma rovinami se společnou osou afinity. Další možností je zvolit si průmětnu π a směr sπ a promítnout osovou afinitu mezi dvěma rovinami ve směru sπ do roviny π (viz následující obrázek). Směr sπ ovšem nelze volit zcela libovolně, musí být různý od směru osové afinity (jinak bychom dostali identitu) a nesmí být rovnoběžný se žádnou z rovin ρ1, ρ2. Rovinu π lze volit libovolně s jedinou výjimkou, nesmí být rovnoběžná se zvoleným směrem promítání sπ. Za rovinu π je možno zvolit i jednu z rovin ρ1, ρ2. Tímto promítáním vznikne geometrická příbuznost mezi body roviny π - osová afinita v rovině.
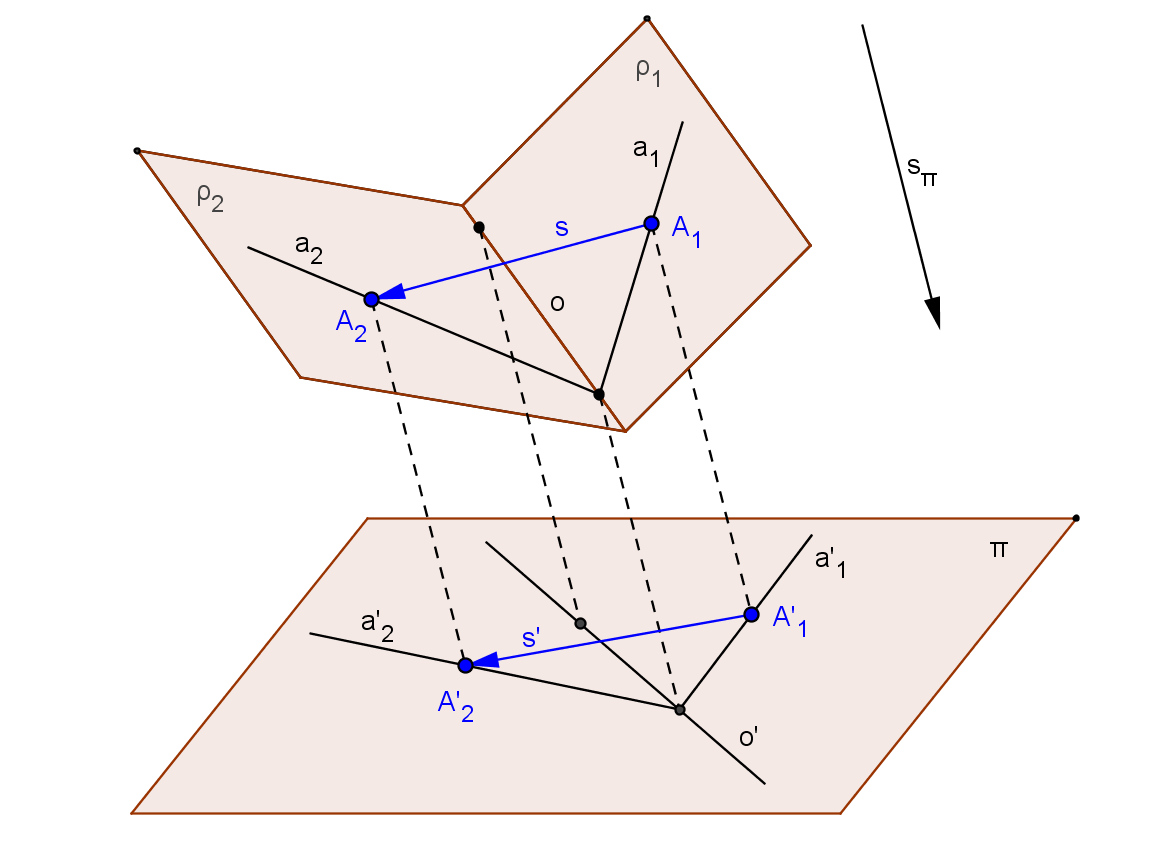
Osa o se promítne do přímky o', body A1, A2 do bodů A'1, A'2, směr afinity s, určený dvojicí bodů A1A2 se tedy promítne do směru s', určeného dvojicí bodů A'1A'2. Osová afinita v rovině bude určena osou o' a dvojicí odpovídajících si bodů A'1, A'2.
Díky tomto způsobu zavedení je lépe vidět, proč lze osovou afinitu využívat při řezech těles.
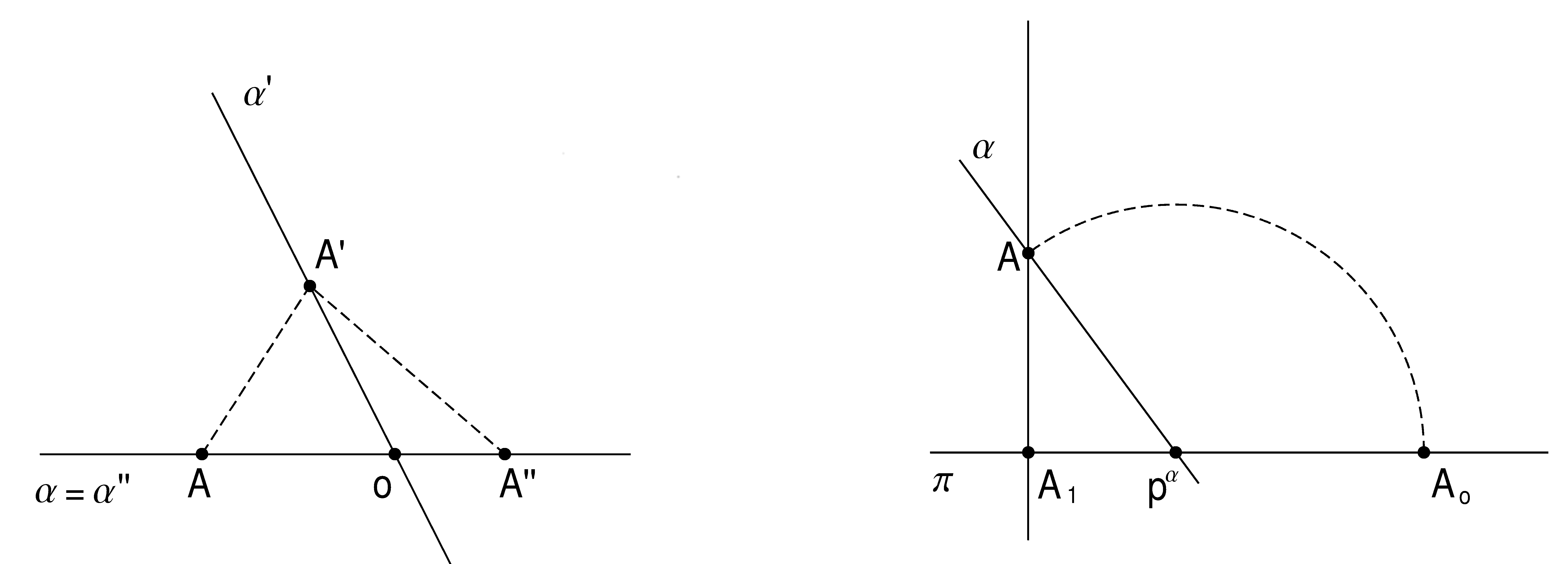
K osové afinitě v rovině můžeme dojít také "zobecňováním osové souměrnosti" v rovině. V rovině je osová souměrnost speciálním případem osové afinity. Vzory (A) a obrazy (A') bodů v osové souměrnosti splňují dvě základní pravidla. Spojnice AA' je kolmá k ose afinity a střed úsečky AA' leží na ose afinity. Ztratí-li se kolmost, získáme zobrazení, které se nazývá šikmé zrcadlení. Ztratíme-li navíc míru, získáváme osovou souměrnost (viz následující obrázky).
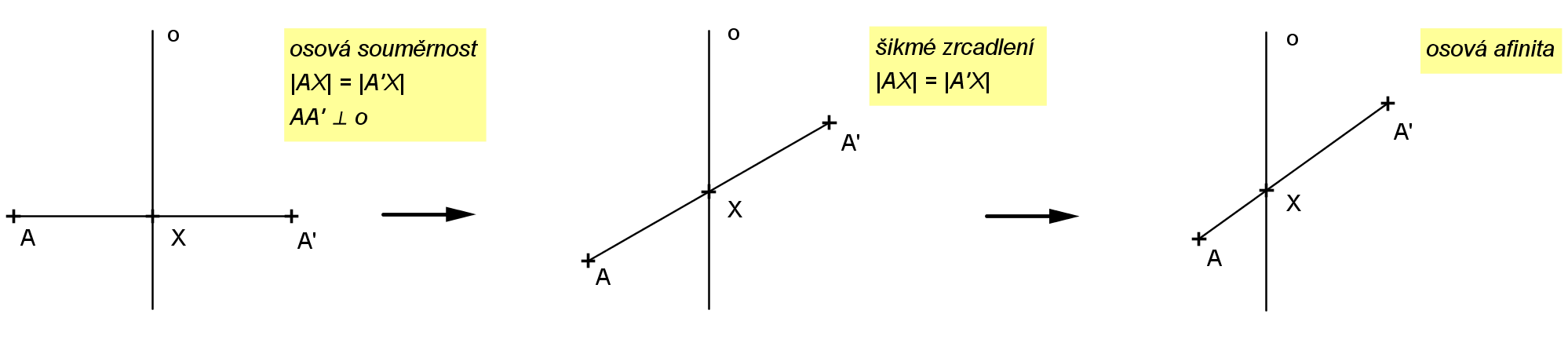
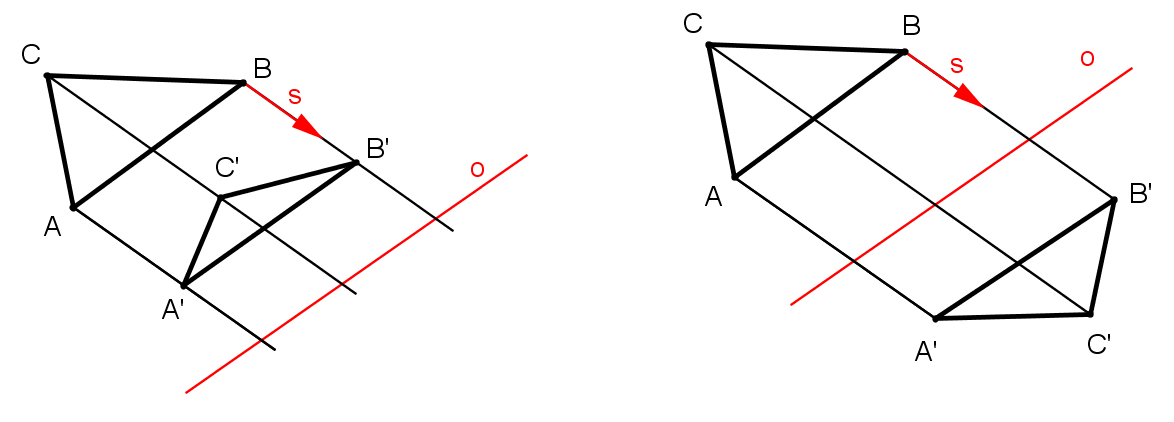
Afinity dělíme na přímé a nepřímé. Podobně jako u shodností jsou přímé afinity takové, které zachovávají orientaci křivek (viz levý obrázek), zatímco nepřímé orientaci křivek mění (viz pravý obrázek). U nepřímých shodností jsme též říkali, že zobrazovaný objekt "převrací z lícu na rub". U osové afinity se až na výjimky tvar objektu deformuje, ale při troše fantazie to tak také můžeme chápat.
Dále můžeme afinity dělit podle velikosti úhlu, který svírá směr afinity s osou na pravoúhlé (s⊥o), kosoúhlé (směr není kolmý ani rovnoběžný s osou) a afinní elaci (s||o). Speciálním případem pravoúhlé afinity je např. osová souměrnost, mezi kosoúhlé afinity patří např. šikmé zrcadlení.
Věta: Osová souměrnost, šikmé zrcadlení a afinní elace jsou plochojevná zobrazení.
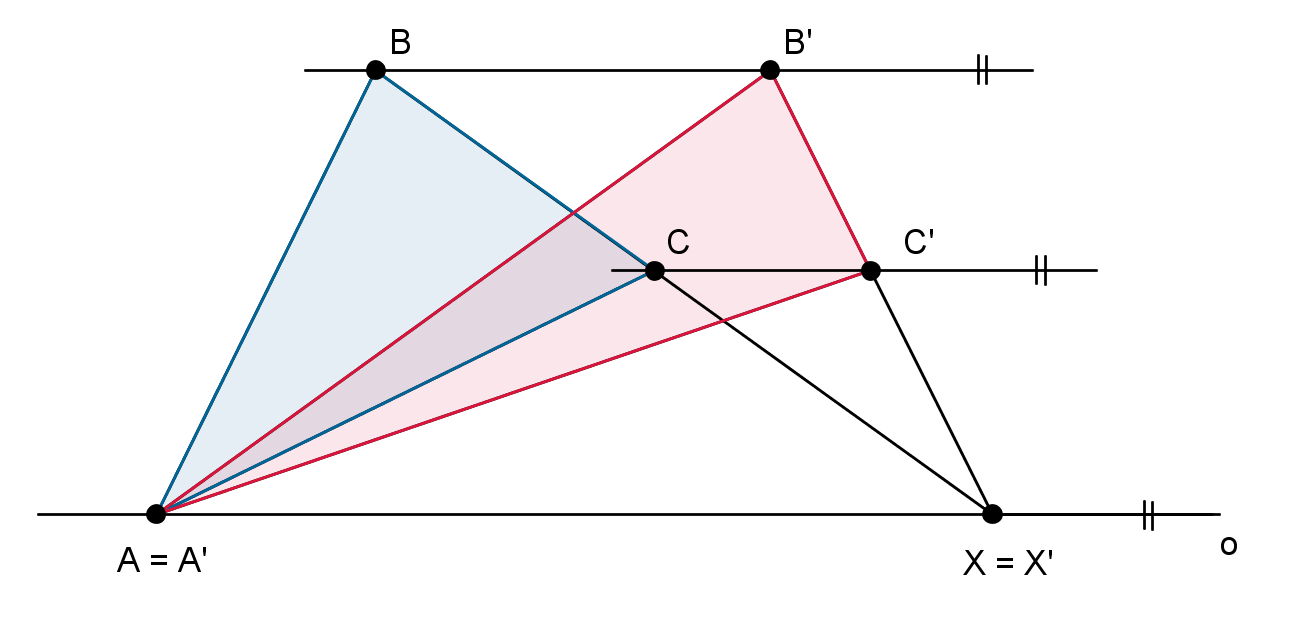Důkaz: Plochojevné zobrazení je takové, které zachovává obsah zobrazovaného útvaru (ovšem nemusí zachovávat tvar). Všechna shodná zobrazení jsou plochojevná, tuto vlastnost má tedy i osová souměrnost. Ukážeme si, jak by se věta dokazovala např. pro obraz trojúhelníku v afinní elaci. Důkaz pro šikmé zrcadlení by byl obdobný. Na obrázku vpravo je sestrojen obraz A'B'C' trojúhelníku ABC v afinní elaci. Z vlastností elace plyne BB' || CC' || o. Označme X = X' samodružný bod přímky BC. Trojúhelníky ABX a A'B'X' mají stejnou základnu i výšku a tedy i stejný obsah. Totéž platí i pro trojúhelníky ACX a A'C'X'. Odtud již snadno odvodíme, že se též rovnají obsahy trojúhelníků ABC a A'B'C'. ■
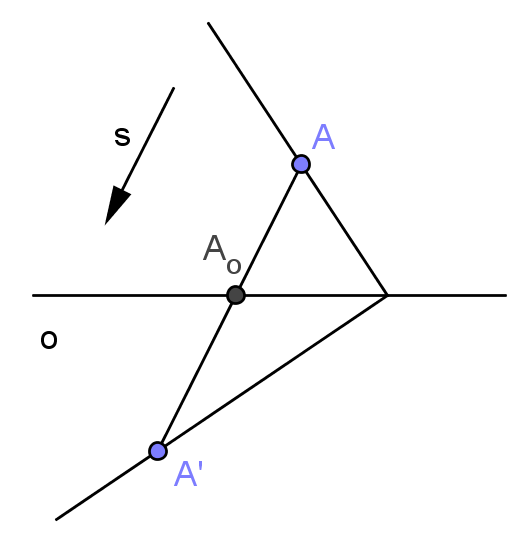
Nechť A je nesamodružný bod dané afinity, A' jeho obraz a Ao průsečík přímky AA' s osou afinity. Dělicí poměr k = (AA'Ao), pro který platí k ≠ 0, 1, nazýváme charakteristikou afinity.
Je-li k < 0, pak sobě odpovídající body leží v téže polorovině určené osou afinity (přímá afinita).
Je-li k > 0, pak odpovídající si body leží v opačných polorovinách (nepřímá afinita).
Pravoúhlá afinita s charakteristikou -1 je osovou souměrností.
Věta: Mějme dánu osovou afinitu, která není elací, osou o a dvojicí odpovídajících si bodů A, A'. Označme Ao průsečík přímky AA' s osou o. Potom pro libovolný bod X, jeho obraz X' a příslušný bod Xo (XX' ∩ o) platí (XX'Xo) = (AA'Ao).
Důkaz:
1) XX' ∉ AA'
a) XA není rovnoběžno s osou (obrázek vlevo)
Označme R samodružný bod přímek XA, X'A'. Středové promítání (z bodu R) na dvě rovnoběžné přímky zachovává dělicí poměr, platí tedy (XX'Xo) = (AA'Ao)
b) XA || o (obrázek vpravo)
X'A' je též rovnoběžno s osou. Rovnoběžné promítání zachovává dělicí poměr, věta tedy platí i v tomto případě.
2) XX' ∈ AA'
Dle (1) věta platí pro libovolnou dvojici bodů B, B', BB' ∉ AA'. Odtud dostáváme (AA'Ao) = (BB'Bo) = (XX'Xo). ■
Osovou afinitu, která není elací, je možno jednoznačně určit osou, směrem a charakteristikou.
Další možné způsoby určení osové afinity v rovině:
• Tři páry odpovídajících si bodů (přičemž odpovídající si body leží na navzájem rovnoběžných přímkách)
• Dva páry odpovídajících si různoběžných přímek
• Dva páry odpovídajících si rovnoběžných přímek a směr afinity
• Osa afinity jeden pár odpovídajících si přímek a směr afinity
• Přímka, bod ležící mimo ni a jejich obrazy
• Dva páry odpovídajících si bodů ležících na rovnoběžných přímkách a charakteristika afinity
Zde najdete příklady na procvičení různých způsobů zadání osové afinity.
Využití osové afinity
S osovou afinitou se v deskriptivní geometrii potkáváme na každém kroku. Využíváme ji hodně při konstrukcích elipsy, z nichž řada je přímo založena na afinním vztahu kružnice a elipsy (trojúhelníková konstrukce, Rytzova konstrukce, příčková konstrukce, ...), můžeme ji využít i při řešení úloh o elipse a přímce (průsečík přímky s elipsou, konstrukce tečen). Více o tom naleznete v kapitole Kuželosečky. Další široké uplatnění má osová afinita při řezech hranolů a válců. V neposlední řadě budeme afinitu využívat při každém otáčení roviny do průmětny (či do jiné roviny) v rovnoběžných promítáních, kde nám její použití ušetří spoustu času a čar.Zde najdete řešené příklady na využití osové afinity.
Středová kolineace mezi dvěma rovinami
Je-li střed kolineace mezi dvěma různoběžnými rovinami vlastním bodem, který není incidentní se žádnou se zvolených rovin, nazývá se příbuznost, kterou získáme tímto středovým promítáním, perspektivní či středovou kolineací mezi dvěma rovinami.
Střed promítání S nazýváme středem kolineace.
Průsečnice o obou rovin je osou kolineace.
Středová kolineace mezi dvěma rovinami je určena, jsou-li dány roviny ρ1, ρ2 a střed S.
Věta: Dvojice bodů sdružených ve středové kolineaci, leží na přímkách procházejících středem kolineace.
Věta: Nesamodružné přímky, které si odpovídají ve středové kolineaci, se protínají na ose kolineace.
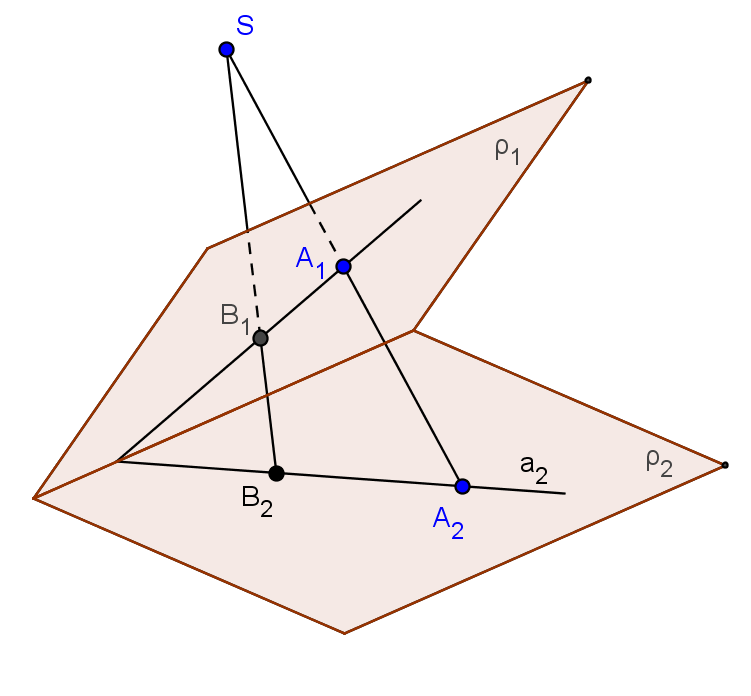
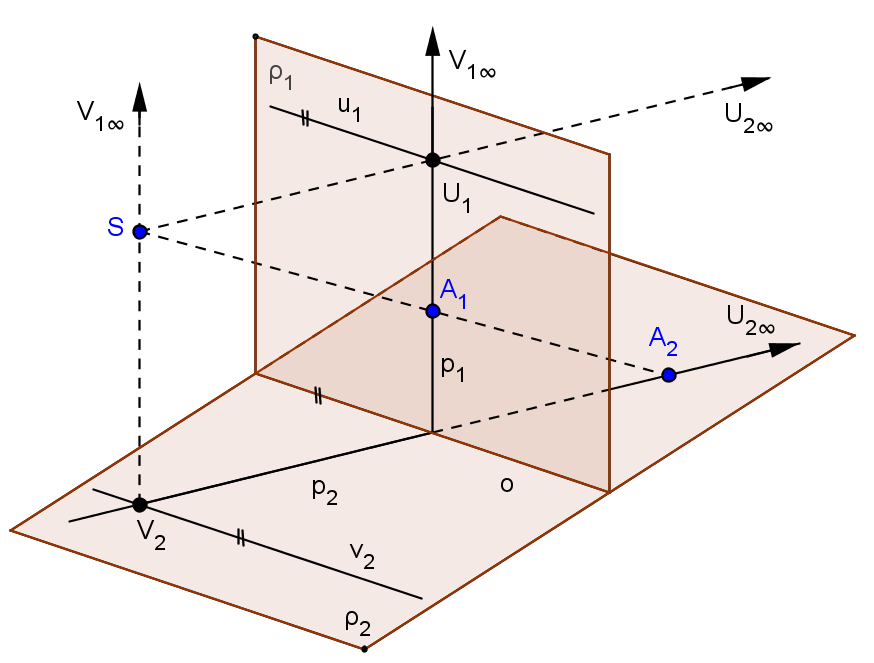
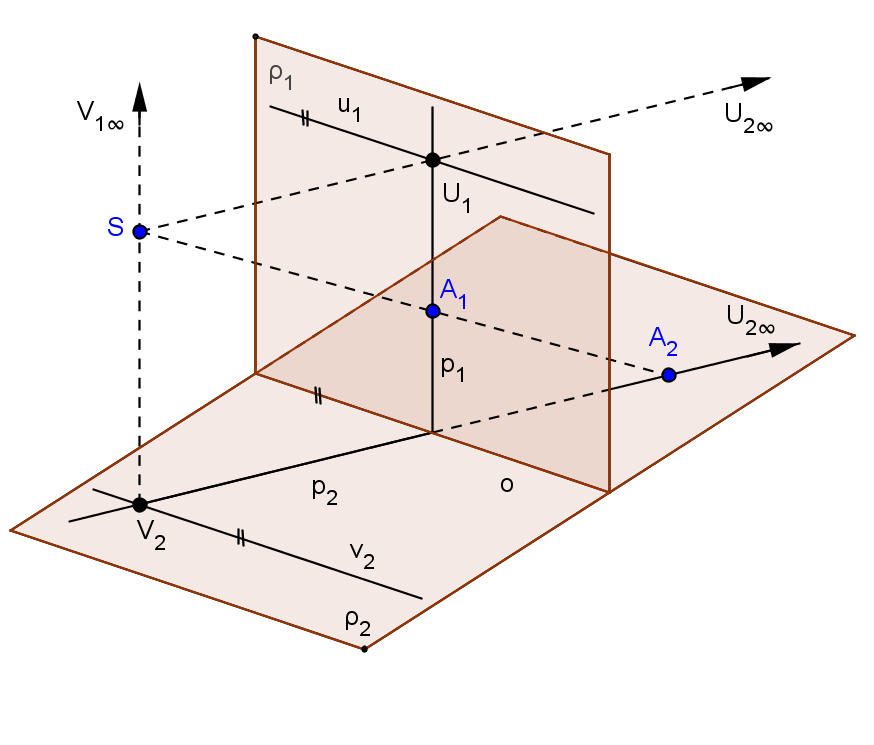
Středová kolineace, na rozdíl od osové afinity nezachovává nevlastní prvky (viz obrázek vpravo nahoře). Obrazem vlastního bodu (přímky), může být i nevlastní bod (přímka). Do nevlastního bodu se zobrazí každý bod U1 roviny ρ1, pro který je spojnice SU1 rovnoběžná s rovinou ρ2. Všechny takové body U1 roviny ρ1 vyplní přímku u1, která je rovnoběžná s rovinou ρ2, tj. je současně rovnoběžná s osou kolineace o. Těmto bodům říkáme úběžníky roviny ρ1, přímku u1 nazýváme úběžnicí roviny ρ1. Pro každý jiný bod A1, ležící mimo u1 platí, že spojnice SA1 není rovnoběžná s rovinou ρ2 a tedy protne tuto rovinu ve vlastním bodě. Obdobně existují v rovině ρ2 body, jejichž vzory v rovině ρ1 jsou nevlastími body (V2 - úběžník roviny ρ2). Všechny tyto body roviny ρ2 opět leží na přímce (v2 - úběžnice roviny ρ2) rovnoběžné s osou kolineace o. V některých učebnicích jsou používány pojmy úběžník, úběžnice pro rovinu ρ1 a protiúběžník, protiúběžnice pro rovinu ρ2.
Středová kolineace v rovině
| Ke stažení: příklady na procvičení látky série 1, série 2 |
Uvažujme středovou kolineaci mezi dvěma rovinami ρ1, ρ2, zprostředkovanou středem promítání S. Zvolme si průmětnu π a směr sπ tak, aby směr sπ nebyl rovnoběžný se žádnou z rovin ρ1, ρ2, π (za rovinu π je možno zvolit i jednu z rovin ρ1, ρ2). Promítneme-li středovou kolineaci mezi dvěma rovinami rovnoběžně ve směru sπ do roviny π, získáme středovou kolineaci v rovině. Označíme-li takto získané průměty čárkou (viz obrázek níže), vidíme, že i nadále platí
S' ∈ A'1A'2
a'1∩a'2 ∈ o'
zachovává se incidence bodů a přímek.
Poznámka: SK v rovině můžeme získat i promítnutím SK mezi dvěma rovnami z vlastního středu O do roviny π (O∉ρ1, ρ2, π, O≠S)
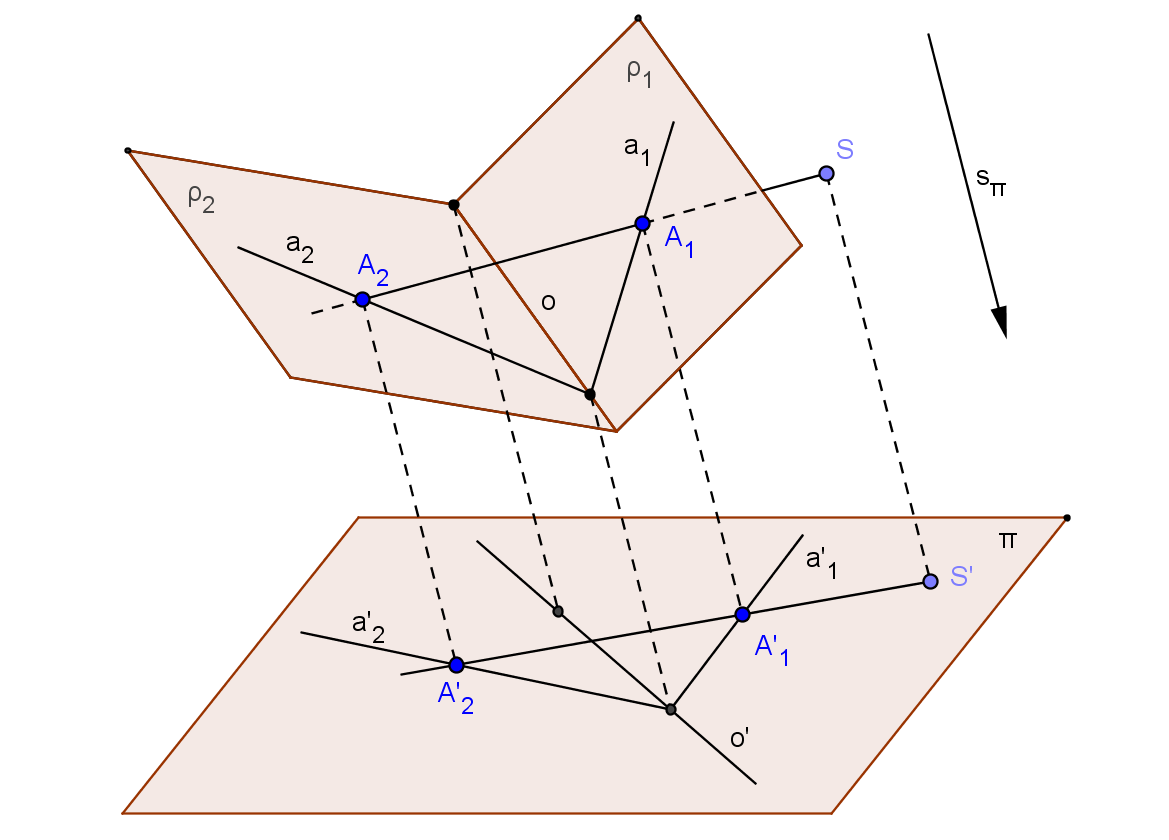
Středová kolineace v rovině je tedy kolineace, jejíž střed i osa jsou vlastní.
Průmět S' bodu S je samodružným bodem středové kolineace v rovině, průmět o' osy o je samodružnou přímkou kolineace v rovině.
Věta: Přímky odpovídající si ve středové kolineaci v rovině se protínají na ose kolineace, odpovídající si body leží na přímkách procházejících středem kolineace.
Bod, který odpovídá nevlastnímu bodu přímky p' se nazývá úběžník přímky p.
Přímka, která odpovídá nevlastní přímce jednoho pole (jedné soustavy bodů) se nazývá úběžnice druhého pole. Obě úběžnice jsou rovnoběžné s osou o, neboť nevlastní přímka roviny a jí odpovídající vlastní přímka mají společný bod v nevlastním bodě osy o.
Středová kolineace v rovině je určena, je-li dáno např.:
• Tři páry odpovídajících si bodů (přičemž spojnice odpovídajících si bodů procházejí jedním bodem)
• Osa kolineace a dva páry odpovídajících si bodů (ležící na různoběžných přímkách)
• Střed kolineace, osa kolineace a dvojice odpovídajících si bodů (ležící na přímce procházející středem)
• Střed kolineace, osa kolineace a dvojice odpovídajících si přímek
• Střed kolineace a dva páry odpovídajících si přímek (spojnice odpovídajících si průsečíků prochází středem kolineace)
• Střed, osa a úběžnice
Zde najdete další možné způsoby zadání SK v rovině a příklady na procvičení.
Využití Středové kolineace
Využití středové kolineace v deskriptivní geometrii je podobné jako u osové afinity. Můžeme ji využít při konstrukcích kuželoseček, pro řezy jehlanů a kuželů, a v neposlední řadě též při otáčení roviny ve středových promítáních.Zde najdete teorii k obrazu kružnice ve středové kolineaci a zde pak řešené příklady na využití středové kolineace.