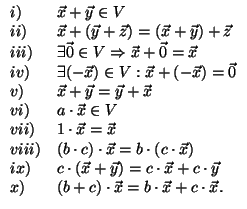
Poznámka: Vektory budeme v následujícím výkladu chápat jako
Definice 1: Nechť ![]() je množina objektů (vektorů),
je množina objektů (vektorů), ![]() je
množina komplexních čísel, + je operace součtu a
je
množina komplexních čísel, + je operace součtu a ![]() je
operace násobení. Pak se čtveřice
je
operace násobení. Pak se čtveřice
![]() nazývá
komplexní vektorový prostor, jestliže pro zmíněné operace platí:
mějme dány libovolné vektory
nazývá
komplexní vektorový prostor, jestliže pro zmíněné operace platí:
mějme dány libovolné vektory
![]() a komplexní čísla
a komplexní čísla
![]() , pak:
, pak:
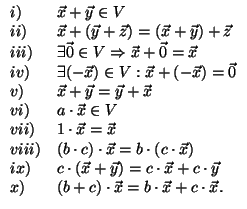
Poznámka: Vektory budeme v následujícím výkladu chápat jako ![]() -rozměrné prvky
-rozměrné prvky ![]() .
.
Definice 2: Komplexní skalární součin na vektorovém prostoru přiřazuje libovolným dvěma vektorům
![]() komplexní číslo, které zapisujeme
komplexní číslo, které zapisujeme
![]() , a které má pro libovolné
, a které má pro libovolné
![]() a
a
![]() tyto vlastnosti:
tyto vlastnosti:
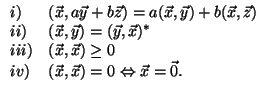
Prostory, v nichž je definován skalární součin se nazývají unitární.
Pro případ vektorů z
![]() navíc platí následující: mějme dva
vektory
navíc platí následující: mějme dva
vektory
![]() . Potom podmínky z definice
skalárního součinu jsou splněny pro
. Potom podmínky z definice
skalárního součinu jsou splněny pro
![]() , kde
, kde ![]() jsou příslušné složky obou vektorů.
Dále říkáme, že jsou dva
vektory
jsou příslušné složky obou vektorů.
Dále říkáme, že jsou dva
vektory
![]() vzájemně ortogonální, pokud je
vzájemně ortogonální, pokud je
![]() . Ortogonální bází potom nazýváme množinu
lineárně nezávislých vektorů, jejíž jakékoliv dva různé vektory mají
skalární součin roven nule. Příkladem může být množina dvou vektorů z
. Ortogonální bází potom nazýváme množinu
lineárně nezávislých vektorů, jejíž jakékoliv dva různé vektory mají
skalární součin roven nule. Příkladem může být množina dvou vektorů z
![]() , kde
, kde
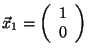 ,
,
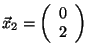 .
.
Definice 3: Každý vektor ![]() má k sobě přiřazeno číslo
má k sobě přiřazeno číslo
![]() , které představuje jeho normu (délku).
Pro jakékoliv vektory
, které představuje jeho normu (délku).
Pro jakékoliv vektory
![]() a číslo
a číslo
![]() platí,
že:
platí,
že:
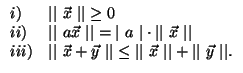
Triviálně dále platí, že
![]() . Vektorový prostor, jenž má normu se nazývá
normovaný vektorový prostor. Pokud je v komplexním vektorovém prostoru
definován skalární součin, pak lze normu vyjádřit jako:
. Vektorový prostor, jenž má normu se nazývá
normovaný vektorový prostor. Pokud je v komplexním vektorovém prostoru
definován skalární součin, pak lze normu vyjádřit jako:
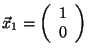 ,
,
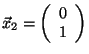 .
Pomocí skalárního součinu můžeme rovněž rozkládat vektory do báze. Pro
ortogonální bázi vektorů
.
Pomocí skalárního součinu můžeme rovněž rozkládat vektory do báze. Pro
ortogonální bázi vektorů
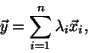
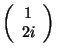 a
a
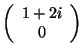 ,
,
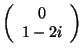 . Snadno nejprve ověříme, že báze je ortogonální, protože
. Snadno nejprve ověříme, že báze je ortogonální, protože
Definice 4: Posloupnost vektorů
![]() normovaného vektorového prostoru se nazývá Cauchyho posloupnost pokud
normovaného vektorového prostoru se nazývá Cauchyho posloupnost pokud
![]() takové, že pro všechny
takové, že pro všechny ![]() je
je
![]() .
.
Definice 5: Vektorový prostor ![]() je úplný, pokud každá Cauchyho
posloupnost vektorů
je úplný, pokud každá Cauchyho
posloupnost vektorů ![]() konverguje k vektoru, který je prvkem
konverguje k vektoru, který je prvkem ![]() .
.
Příklad 2:
Cauchyho posloupnost se skládá z čísel, jejichž rozdíly se s vyšším
indexem čísel posloupnosti zmenšují. Například posloupnost
![]() je Cauchyho posloupnost
racionálních čísel. Vidíme, že prostor racionálních čísel není úplný, protože
tato posloupnost konverguje zřejmě k
je Cauchyho posloupnost
racionálních čísel. Vidíme, že prostor racionálních čísel není úplný, protože
tato posloupnost konverguje zřejmě k ![]() , jenž není racionální číslo.
, jenž není racionální číslo.
Motivací pro zavedení úplnosti Hilbertova prostoru v kvantové informatice je požadavek na vývoj izolovaného kvantového stavu v rámci jednoho Hilbertova prostoru (to znamená, že chceme, aby vývoj stavu konvergoval také do jistého stavu).
Poznámka: Pojem konvergence (limity) vychází ze zavedení metriky prostoru
(vzdálenosti mezi dvěma prvky) jako
![]() .
.
Definice 6: Úplný unitární vektorový prostor se nazývá
Hilbertův prostor ![]() .
.
V roce 1932 vyšla v němčině kniha matematika Johna von Neumanna, který v ní popis kvantových systémů zformalizoval.
Postulát 1: Stavy kvantového systému korespondují vektorům Hilbertova prostoru.
V kvantové mechanice se stav zapisuje v tzv. Diracově notaci,
která pro zápis vektoru ![]() používá ekvivalentu
používá ekvivalentu
![]() a nazývá jej ket. Vektory Hilbertova
prostoru (které stále chápeme jako aritmetické)
zapisujeme buď v řádku nebo sloupci. Jestliže jsou
sloupcové vektory prvky prostoru
a nazývá jej ket. Vektory Hilbertova
prostoru (které stále chápeme jako aritmetické)
zapisujeme buď v řádku nebo sloupci. Jestliže jsou
sloupcové vektory prvky prostoru ![]() , pak řádkové vektory představují prvky
tzv. duálního prostoru
, pak řádkové vektory představují prvky
tzv. duálního prostoru ![]() .
Duální (konjugovaný) prostor je prostor lineárních funkcí na vektorovém
prostoru
.
Duální (konjugovaný) prostor je prostor lineárních funkcí na vektorovém
prostoru ![]() . Pokud je pro stavy
. Pokud je pro stavy
![]() definována funkce
definována funkce
![]() jako
jako
![]() , pak
, pak ![]() je
ekvivalentní řádkovému vektoru, který zapisujeme
je
ekvivalentní řádkovému vektoru, který zapisujeme ![]() a nazýváme
bra. Lze ukázat, že pro vektory z
a nazýváme
bra. Lze ukázat, že pro vektory z
![]() představují vektory z
představují vektory z ![]() komplexně sdruženou transpozici k
vektorům z
komplexně sdruženou transpozici k
vektorům z ![]() .
S jejich pomocí lze pro dva vektory
.
S jejich pomocí lze pro dva vektory
![]() odpovídající stavům
odpovídající stavům ![]() a
a ![]() definovat skalární součin jako
definovat skalární součin jako
![]() , což se obvykle zkracuje na zápis
, což se obvykle zkracuje na zápis
![]() tvořící závorku (bracket).
Shrňme si notaci do následující tabulky:
tvořící závorku (bracket).
Shrňme si notaci do následující tabulky:
|
Příklad 3: Obecný ket ![]() =
=
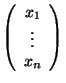 má příslušný vektor bra
má příslušný vektor bra
![]() kde symbol
kde symbol ![]() označuje komplexně-sdruženou transpozici.
označuje komplexně-sdruženou transpozici.
Příklad 4: Uvažujeme-li tří-složkové vektory
![]() ,
pak skalární součin generuje skalár:
,
pak skalární součin generuje skalár:
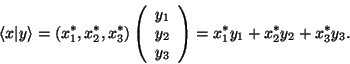
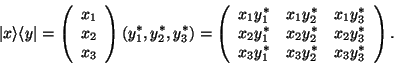
Pro každý uzavřený podprostor ![]() v
v ![]() existuje jeho komplementární
podprostor
existuje jeho komplementární
podprostor ![]() , který obsahuje prvky kolmé k prvkům
, který obsahuje prvky kolmé k prvkům ![]() (tj.
(tj.
![]() , pokud je
, pokud je
![]() ).
Navíc každý vektor
).
Navíc každý vektor
![]() lze vyjádřit ve tvaru
lze vyjádřit ve tvaru
![]() kde
kde
![]() . Obecně je možné vyjádřit dekompozici prostoru
. Obecně je možné vyjádřit dekompozici prostoru
![]() pomocí jeho
pomocí jeho ![]() ortogonálních podprostorů jako:
ortogonálních podprostorů jako:
![]() , kde
, kde ![]() představuje direktní součet.
představuje direktní součet.
Definice 8:
Lineární operátor A:
![]() přiřazuje každému vektoru
přiřazuje každému vektoru
![]() vektor
A
vektor
A
![]() , kde
, kde
![]() a
a
![]() platí, že
platí, že
![]() .
.
Lineární operátory tedy umožňují transformovat vektory v jednom prostoru.
Pokud operátor A působí na vektory duálního prostoru,
potom takovou operaci zapisujeme ![]() A.
Elementy matice lineárního operátoru můžeme rovněž vyjádřit pomocí bázových
vektorů jako A
A.
Elementy matice lineárního operátoru můžeme rovněž vyjádřit pomocí bázových
vektorů jako A![]() =
=
![]() , kde
, kde ![]() jsou indexy řádků a sloupců a množina
jsou indexy řádků a sloupců a množina
![]() je báze indexovaná stejně jako řádky.
Operátor, který zobrazuje vektory na sebe samy se nazývá jednotkový a
značí se 1. Je definován pomocí bázových vektorů
je báze indexovaná stejně jako řádky.
Operátor, který zobrazuje vektory na sebe samy se nazývá jednotkový a
značí se 1. Je definován pomocí bázových vektorů
![]() jako
jako
![]() .
Pro ortonormální bázi se zřejmě jedná o jednotkovou matici.
.
Pro ortonormální bázi se zřejmě jedná o jednotkovou matici.
Definice 9: Operátor
![]() se nazývá sdružený
(adjungovaný) k operátoru A, jestliže
pro všechny
se nazývá sdružený
(adjungovaný) k operátoru A, jestliže
pro všechny
![]() platí, že
platí, že
![]() .
.
Pro popis fyzikálních veličin (pozorovatelných veličin) používá kvantová mechanika zvláštní třídu tzv. Hermitových operátorů.
Definice 10: Operátor A se nazývá samosdružený
(také Hermitový), jestliže pro všechny
![]() platí, že
platí, že
![]() , tj.
, tj.
![]() .
.
Definice 11: Lineární operátor A má vlastní
vektory
![]() a vlastní hodnoty
a vlastní hodnoty ![]() , kde
, kde
![]() ,
resp.
,
resp.
![]() .
.
Pro výpočet vlastních hodnot si všimněme, že determinant
det
![]() .
V případě Hermitových operátorů, jsou všechny vlastní hodnoty reálné.
Ty korespondují všem (také reálným) možným výsledkům měření určité veličiny.
Odpovídající vlastní vektory jsou přitom navzájem ortogonální.
.
V případě Hermitových operátorů, jsou všechny vlastní hodnoty reálné.
Ty korespondují všem (také reálným) možným výsledkům měření určité veličiny.
Odpovídající vlastní vektory jsou přitom navzájem ortogonální.
Postulát 2: Pozorovatelné fyzikální veličiny se popisují Hermitovými operátory, jejichž reálné vlastní hodnoty odpovídají možným výsledkům měření.
Vlastní vektory Hermitových operátorů operujících na prostoru ![]() tvoří
jeho bázi, tj. všechny vektory
tvoří
jeho bázi, tj. všechny vektory
![]() lze vyjádřit jako
lze vyjádřit jako
![]() , kde
, kde
![]() jsou vlastní
vektory a
jsou vlastní
vektory a
![]() jsou příslušné koeficienty.
jsou příslušné koeficienty.
Definice 12: Unitární lineární operátor U
provádí zobrazení celého prostoru ![]() na sama sebe a pro vektory
na sama sebe a pro vektory
![]() platí, že
platí, že
![]() .
.
Poslední podmínka znamená, že aplikace unitárního operátoru nemění
skalární součin obou vektorů a můžeme ji také zapsat jako
![]() .
.
Nyní máme nadefinovány základní pojmy, které budeme používat. K ostatním se dostaneme při výkladu konkrétních problémů. Protože jsme se zatím kromě důležitých sdělení v postulátech nedozvěděli, jak kvantová mechanika s tímto matematickým formalizmem souvisí, musíme si nyní o tomto vztahu povědět více. Začněme popisem kvantového stavu a problematickou otázkou měření kvantového systému.