Shorův faktorizační algoritmus

Jak bylo uvedeno, klasická kryptografie je vzhledem k možnostem počítačů v této chvíli bezpečnou formou zabezpečení přenosu dat. Jak si ale s problémem prolomení metody RSA poradí kvantový počítač? Má jednu velkou výhodu - může totiž využít kvantového paralelismu. Algoritmus Petera Shora na faktorizaci velkých celých čísel právě tuto vlastnost kvantových systémů využívá. Na kvantovém počítači tento algoritmus běží v asymptotickém čase ${\cal O} (L^2 \mathrm {log}\ L\ \mathrm {log\ log}\ L)$, kde $L$ je počet bitů faktorizovaného čísla. Vidíme, že čas je omezen shora polynomem. Místo, aby algoritmus hledal přímo jednotlivé součinitele, je spíše založen na poznatku, že problém faktorizace čísel se dá převést na problém hledání periody určité periodické funkce. Je-li dáno číslo $n$, které chceme faktorizovat, je potřeba vytvořit periodickou funkci

$$f_{y,n} (a) = y^a \mathrm {mod}\ n,$$

kde $y$ je náhodné celé číslo nesoudělné s $n$. Na této funkci je zajímavá její periodicita. Její perioda modulo $n$ se obvykle značí $r$. Protože je každá $r$-tá hodnota funkce stejná ( $f_{y,n}(a) = f_{y,n} (a + r)$), platí

$$y^r \equiv 1\ \mathrm {mod}\ n.$$

To lze upravit na tvar

$$(y^{r/2} - 1)(y^{r/2} + 1) \equiv 0\ {\rm mod}\ n.$$

Tento vztah platí pro sudou periodu $r$ (pro lichou se snažíme náhodně vybrat jinou hodnotu $y$ - viz příklad níže). Z tohoto tvaru vidíme, že dělení členů na levé straně rovnice číslem $n$ je bezezbytkové. Proto, pokud není triviálně $y^{r/2} \equiv \pm 1\ \mathrm {mod}\ n$, pak musí mít některý z členů na levé straně společný faktor s $n$. Tímto krokem se vlastně úloha převádí na problém hledání největšího společného dělitele (nsd) čísel $(y^{r/2} - 1, n)$ a $(y^{r/2} + 1, n)$. Na tento problém existuje algoritmus běžící efektivně i na klasických počítačích. Následující příklad by měl problém objasnit.

Příklad: Řekněme, že chceme faktorizovat číslo 21 na součin jeho prvočinitelů. Pokud je $n = 21$, pak si musíme zvolit $1 < y < 21$ takové, že $nsd\ (y, 21) = 1$. Odpovídající množina čísel $y$ je {2, 4, 5, 8, 10, 11, 13, 16, 17, 19, 20}. Z ní si náhodně zvolíme například $y = 10$. Nyní chceme zjistit periodu funkce $f_{y,n} (a) = 10^a {\rm mod}\ 21$. Vidíme, že funkční hodnoty pro celé $a = 1, 2, \ldots$ jsou $10, 16, 13, 4, 19, 1, 10, 16, \ldots$. To znamená, že tato funkce má periodu 6. Tato perioda je sudá a nevrací triviální faktory (Jestliže $y^{r/2} = 1000$, pak chceme ověřit, zda $1000 \equiv^? \pm 1\ ({\rm mod}\ 21)$. To neplatí, protože $999 \nmid 21$ a $1001 \nmid 21$. Pokud by se tak stalo, museli bychom zvolit jiné $y$.). Na závěr nalezneme faktory pomocí $nsd\ (1001, 21) = 7$ a $nsd\ (999, 21) = 3$. Všimněme si, že pro $y = 20$ algoritmus neuspěje, protože perioda $r = 2$. Zajímá nás tedy, zda $20 \equiv^? \pm 1\ ({\rm mod}\ 21)$ a vidíme, že $21 \mid 21$.

Nyní nám zbývá jediný problém - jak vypočítat efektivně periodu $r$ dané funkce. Tento problém není klasicky řešitelný v polynomiálním čase. Shor ale ukázal, že na kvantovém počítači periodu efektivně nalézt lze. Toho dosáhl využitím kvantového paralelismu. Připravme si kvantový registr, který bude mít 2 části nazvané $R1$ a $R2$, a jehož stav budeme zapisovat $\vert r1, r2 \rangle$.

krok 1: Zvolíme si náhodně $y$, které je nesoudělné s $n$. Dále si vybereme $q$ takové, že $2n^2 \le q \le 3n^2$.
krok 2: Připravíme kvantový registr do superpozice čísel $\vert\psi\rangle$ tak, že v $R1$ máme superpozici čísel 0 až $q - 1$, a v $R2$ samé nuly. Registr tak přejde do stavu

$$\vert\Psi \rangle = \frac{1}{\sqrt{q}}\sum_{a=0}^{q-1} \vert a,0\rangle.$$

krok 3: Z hodnot v $R1$ vypočteme (paralelně) funkční hodnoty funkce $f_{y,n}(a)$ a zapíšeme je do $R2$.

$$\vert\Psi \rangle = \frac{1}{\sqrt{q}}\sum_{a=0}^{q-1} \vert a,y^a\mathrm{mod}\ n\rangle.$$

krok 4: Nyní změříme pouze část $R2$ registru jako hodnotu $k$. Tím uvedeme celý registr do superpozice čísel, které mají funkční hodnotu $k$ a představují projekci registru, v němž předtím byly vyváženě zastoupeny všechny hodnoty periodické funkce $f_{y,n}(a)$.

$$\vert\Psi \rangle = \frac{1}{\sqrt{\vert A\vert}}\sum_{a' \in A}\vert a',k\rangle,$$

kde $A = \{a':y^{a'} {\rm mod}\ n = k\}$ a $\vert A\vert$ je počet prvků množiny $A$. Použijme nyní příkladu s faktorizací čísla 21 a uvědomme si, v jakém stavu se registr před tímto krokem nacházel. Po 3. kroku byl registr v superpozici $\frac{1}{\sqrt{22}} (\vert,1\rangle + \vert 1,10\rangle + \vert 2,16\rangle + ... ...4\rangle + \vert 5,19\rangle + \vert 6,1\rangle + \ldots + \vert 21,13\rangle)$. Provedením měření podle kroku 4 se vyselektují pouze stavy příslušející naměřené hodnotě (se stejnou vlastní hodnotou). Podle výsledku měření tak dostaneme jednu z 6 možných superpozic:

změřeno	nový stav
1	$\frac{1}{2}(\vert,1\rangle + \vert 6,1\rangle + \vert 12,1\rangle + \vert 18,1\rangle)$
10	$\frac{1}{2}(\vert 1,10\rangle + \vert 7,10\rangle + \vert 13,10\rangle + \vert 19,10\rangle)$
16	$\frac{1}{2}(\vert 2,16\rangle + \vert 8,16\rangle + \vert 14,16\rangle + \vert 20,16\rangle)$
13	$\frac{1}{2}(\vert 3,13\rangle + \vert 9,13\rangle + \vert 15,13\rangle + \vert 21,13\rangle)$
4	$\frac{1}{\sqrt{3}}(\vert 4,4\rangle + \vert 10,4\rangle + \vert 16,4\rangle)$
19	$\frac{1}{\sqrt{3}}(\vert 5,19\rangle + \vert 11,19\rangle + \vert 17,19\rangle)$

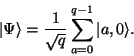
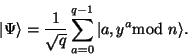
Zdá se, že k odhadu periody z těchto stavů bylo by potřeba první tři kroky několikrát opakovat ke změření několika hodnot. Bohužel to není možné v důsledku různého počátečního offsetu periody u každého výsledku měření. Tento offset nám neumožňuje mít při opakovaných měřeních jistotu, že dosáhneme stejného výsledku a budeme moci periodu určit jednoznačně. To proto, že pravděpodobnosti změření všech 6 výsledků jsou (přibližně¹⁰) stejné. Aby bylo možné periodu správně určit, je zapotřebí ji nějakým způsobem zvýraznit tak, aby nebyla závislá na počátečním offsetu.

krok 5: Proto nyní provedeme kvantovou Fourierovu transformaci na $R1$ a výsledek vrátíme tamtéž.

$$\vert\Psi \rangle = \frac{1}{\sqrt{\vert A\vert}}\sum_{a' \in... ...}{\sqrt{q}} \sum_{c=0}^{q-1} e^{2\pi ia'c/q} \vert c,k \rangle.$$

Fourierova transformace převedla stav registru $\vert a'\rangle$ na $\vert c\rangle$, tentokrát již s různými amplitudami. Ty stavy, které se vyskytují v okolí násobků převrácené periody $1/r$ tak naměříme s větší pravděpodobností než ty, které jsou od násobků více vzdáleny. Důležité je, že stav $\vert a'\rangle$ obsahující problematický offset periody funkce se přesunul do fázového faktoru.

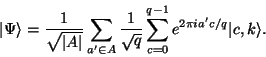
krok 6: Nyní registr změříme s výsledkem $c'$. Abychom byli schopni určit periodu, je nutné kroky 2 - 6 opakovat do chvíle, než máme k dispozici dostatek vzorků, které jsou s velkou pravděpodobností v okolí různých násobků převrácené periody a které jednoznačně umožňují určit periodu. Pokud tyto násobky označíme $\lambda$, pak $c'$ je nějakým násobkem $\lambda$ výrazu $q/r$, tj. $c' = \lambda\frac{q}{r}$. Po úpravě dostaneme $c'/q = \lambda/r$, pro $\lambda \in {\mathbb{Z}}^+$. Odhad, jaký násobek $\lambda$ byl naměřen, se provádí rozvojem $c'/q$ do řetězcového zlomku.

krok 7: Když je známa hodnota $r$, jsou již klasicky Eucleidovým algoritmem vypočteny největší společné dělitele $(y^{r/2} - 1, n)$ a $(y^{r/2} + 1, n)$.

Protože je tento algoritmus pravděpodobnostní povahy, není zaručeno, že na konci dostaneme dva užitečné faktory, které nás zajímají. Například špatná volba $y$ v prvním bodě algoritmu může vést k dosažení triviálních řešení rovnice $(y^{r/2} - 1)(y^{r/2} + 1) \equiv 0\ \mathrm{mod}\ n.$ Vidíme, že Shorův algoritmus je vlastně kombinací dvou metod. Jednak hledání periody funkce $f_{y,n}(a)$ na kvantovém počítači, a jednak hledání největších společných dělitelů dvou čísel na klasickém počítači. Běžící časy obou metod se asymptoticky sčítají pouze na polynomiální složitost. Je možné zhruba odhadnout, že pokud je složitost řádu $L^2$, pak například faktorizace 768 bitového čísla by při délce jednoho výpočetního kroku kolem 100 cyklů trvalo na 100 MHz kvantovém počítači řádově jednotky sekund. Je jasné, že pokud by se podařilo takový algoritmus použít na skutečném kvantovém počítači, dostali bychom do rukou nástroj na prolamování většiny dnes používaných kryptoschémat. Není divu, že se již několik let o postup ve vývoji kvantových počítačů zajímají instituce, jejichž bezpečnostní systémy jsou založeny na složitosti problémů, jako je faktorizace. O tom, v jakém stádiu se vývoj kvantových počítačů nachází a o tom, jaké překážky klade vědcům vlastní implementace kvantového počítače se zmíníme v závěrečné kapitole. Nyní si ale představme, že žijeme v době, kdy již není kvantový počítač jen na papíře a uvědomme si, jak by se asi změnila kryptografie jakou známe s existencí kvantových počítačů. Běžně by bylo možné výše popsaná kryptoschémata prolomit. Pak by nám nezbývalo nic jiného, než se pokusit kvantových systémů využít k vytvoření nových bezpečných komunikačních schémat, která by byla schopná vzdorovat pokusům o jejich prolomení. Proto zvládnutí kvantové mechaniky pro řešení problémů faktorizace neznamená konec kryptografie. Pouze to určitým způsobem mění podstatu používaných mechanizmů. S jedním z nich se seznámíme dále.