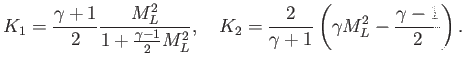Next: About this document ...
The computational domain is
![]() with the periodic extension
in the
with the periodic extension
in the ![]() -direction.
A stationary plane shock wave is located at
-direction.
A stationary plane shock wave is located at ![]() . The prescribed pressure
jump through the shock is
. The prescribed pressure
jump through the shock is
![]() , where
, where ![]() and
and
![]() are the pressure values
from the left and right of the shock wave, respectively, corresponding to
the inlet (left) Mach number
are the pressure values
from the left and right of the shock wave, respectively, corresponding to
the inlet (left) Mach number
![]() .
The reference density and velocity are those of the free uniform flow
at infinity.
In particular, we define the initial density,
.
The reference density and velocity are those of the free uniform flow
at infinity.
In particular, we define the initial density, ![]() -component of velocity and pressure by
-component of velocity and pressure by