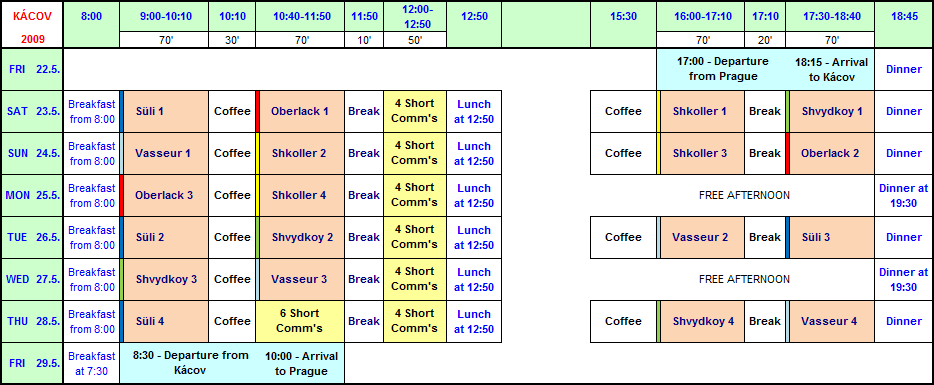
The schedule of the conference

Each main lecturer gives a series of four lectures, each 70 minutes long, except Prof. Oberlack who gives a series of three 70-minutes-long lectures.

The participants can present their results in the framework of
Short Communications (12 minutes each, including discussion)
and within the reprint and preprint exhibition.

The program can be changed during the conference. See the posted information on the conference place.


programme



Abstracts of main lectures

  1. Martin Oberlack

    Centre of Research Excellence Fluid Flow and Combustion
    Technical University Darmstadt
    Petersenstr. 13
    64287 Darmstadt
    Germany
    email: office (at) fdy.tu-darmstadt.de
    home: http://www.fdy.tu-darmstadt.de/en/staff/oberlack.html

    On turbulence theory and modelling

    Abstract:

    The three lectures on turbulence theory and modeling will be given:

    1. Statistical description of turbulence and the closure problem
    2. Turbulent scaling laws using Lie symmetry methods I
    3. Turbulent scaling laws using Lie symmetry methods II

  2. Steve Shkoller

    Department of Mathematics
    University of California
    Davis, CA 95616-8633
    USA
    email: shkoller (at) math.ucdavis.edu
    home: http://www.math.ucdavis.edu/~shkoller/

    Analysis of moving boundary problems for incompressible and compressible three-dimensional perfect fluids

    Abstract:

    The analysis of moving interface problems for inviscid (perfect) 3D fluids is of paramount importance in the study of vortex sheets, shock waves, moving vacuum boundaries, and other propagating surfaces of discontinuity. The fluid flow is governed by the Euler equations, while the motion of the fluid boundary (or material interface) is governed by various components of the fluid velocity, and is thus coupled to the interior motion in a highly nonlinear fashion. These lectures will cover the a priori nonlinear estimates as well as the construction of solutions for the free-surface Euler equations in vacuum, for both incompressible and compressible cases. I will explain how the Lagrangian formulation naturally encodes the geometry of the moving boundary into the Euler equations, and will present a few new technical tools that are necessary for the process of constructing solutions.

  3. Roman Shvydkoy

    Department of Mathematics, Statistics and Computer Science
    University of Illinois at Chicago
    MSCS (m/c 249)
    851 S. Morgan St.
    Chicago, IL 60607-7045
    USA
    email: shvydkoy (at) math.uic.edu
    home: http://www.math.uic.edu/~shvydkoy/

    Lectures on the Onsager conjecture and related topics

    Abstract:

    One of Onsager's many contributions to fluid dynamics is his celebrated conjecture which states that the minimal space regularity needed for a weak solution of the Euler equation to conserve energy is 1/3. In this series of lectures I will give a detailed introduction into the problem. We will discuss quasi-local estimates on the energy flux, their interpretations in terms of scaling laws of turbulence, recent attempts to construct rough dissipative solutions, as well as positive results on energy conservation. If time permits, I will address related questions such as energy equality for Leray-Hopf solutions of the Navier-Stokes equation, partial regularity results in Besov spaces, etc.

  4. Endre Süli

    Oxford University Computing Laboratory
    Wolfson Building, Parks Road
    Oxford OX1 3QD
    UK
    email: Endre.Suli (at) comlab.ox.ac.uk
    home: http://web.comlab.ox.ac.uk/endre.suli/

    Kinetic models for dilute polymers: analysis, approximation and computation

    Abstract:

    We review recent analytical and computational results for macroscopic-microscopic bead-spring models that arise from the kinetic theory of dilute solutions of incompressible polymeric fluids with noninteracting polymer chains, involving the coupling of the unsteady Navier-Stokes system in a bounded domain $\Omega \subset \mathbb{R}^d$, $d=2$ or $3$, with an elastic extra-stress tensor as right-hand side in the momentum equation, and a (possibly degenerate) Fokker-Planck equation over the $(2d+1)$-dimensional region $\Omega \times D \times [0,T]$, where $D \subset \mathbb{R}^d$ is the configuration domain and $[0,T]$ is the temporal domain. The Fokker-Planck equation arises from a system of (It$\hat{\rm o}$) stochastic differential equations, which models the evolution of a $2d$-component vectorial stochastic process comprised by the $d$-component centre-of-mass vector and the $d$-component orientation (or configuration) vector of the polymer chain. We show the existence of global-in-time weak solutions to the coupled Navier--Stokes--Fokker--Planck system for a general class of spring potentials including, in particular, the widely used finitely extensible nonlinear elastic (FENE) potential. The numerical approximation of this high-dimensional coupled system is a formidable computational challenge, complicated by the fact that for practically relevant spring potentials, such as the FENE potential, the drift term in the Fokker-Planck equation is unbounded on $\partial D$. We shall present numerical simulations for this coupled high-dimensional micro-macro model and consider the analysis of the numerical algorithms. The work presented in this lecture series is based on joint research with John W. Barrett (Imperial College London) and David Knezevic (Massachusetts Institute of Technology).

    View this abstract as PDF file.

  5. Alexis F. Vasseur

    Department of Mathematics
    The University of Texas at Austin
    1 University Station, C1200
    Austin, Texas 78712
    USA
    email: vasseur (at) math.utexas.edu
    home: http://www.ma.utexas.edu/users/vasseur/vasseur.html

    The De Giorgi method for regularity of solutions of elliptic equations and its applications to fluid dynamics

    Abstract:

    In 1957, E. de Giorgi solved the 19th Hilbert problem by proving the regularity and analyticity of variational solutions to nonlinear elliptic variational problems. In so doing, he developed a very geometric, basic method to deduce boundedness and regularity of solutions to a priori very discontinuous problems. The essence of his method has found applications in homogenization, phase transition, inverse problems, etc... More recently, it has been successfully applied to several different problems in fluid dynamics. Especially, it has been used to prove the global regularity for solutions of the quasigeostrophic equations in the critical case, for large initial data. This equation was introduced previously by several authors as a toy model for the problem of global regularity of solutions to 3D Navier-Stokes equations. In a first part, we will review the De Giorgi's proof, stressing the important aspects of his approach. In a second part, we will show how to adapt his method to the regularity theory for the quasigeostrophic equation.