Konstrukce
Konstrukce elipsy
Bodová konstrukce I
Bezprostředně z definice elipsy vyplývá tzv. bodová konstrukce I, která je nahrána v apletu E7.1.
Nechť jsou dány dva různé body - ohniska F_1, \, F_2 a délka hlavní poloosy a. Budeme hledat body, které mají konstantní součet vzdáleností rovný 2a od ohnisek F_1, \, F_2. Za tímto účelem si na přímce F_1F_2 sestrojíme hlavní vrcholy A, \, B elipsy, přičemž |AS| = |SB| = a, kde S je středem úsečky F_1F_2 (středem hledané elipsy).Dále budeme volit libovolně bod L \in F_1F_2, jenž úsečku AB rozdělí na dvě části o délkách l_1 = |AL|, \, l_2 = |LB|, \, (l_1 + l_2 = 2a). Sestrojíme kružnice k_{F_1} \, (F_1, \, l_2), \, k_{F_2} \, (F_2, \, l_1) a k'_{F_1} \, (F_1, \, l_1), \, k'_{F_2} \, (F_2, \, l_2). Je zřejmé, že kružnice k_{F_1}, \, k_{F_2} (resp. k'_{F_1}, \, k'_{F_2}) se protínají v bodech elipsy (k_{F_1} \cap k_{F_2} = \{ I, \, II \}, \; k'_{F_1} \cap k'_{F_2} = \{ III, \, IV \}). Různou volbou bodu L získáme různé poloměry kružnic a tím i různé body elipsy.
V apletu E7.1 je konstrukce nahraná. Po přehrání můžete měnit polohu bodu L - pohybovat s ním po úsečce AB, tím získáte další body elipsy.
Aplet E7.1: Bodová konstrukce elipsy I
Pozn.: Pokud bude elipsa zadána délkou hlavní a vedlejší poloosy, pak samozřejmě není problém ohniska dohledat (pomocí charakteristického trojúhelníka) a provést bodovou konstrukci.
Bodová konstrukce II
Další způsob jak sestrojit jednotlivé body elipsy, pokud jsou dány délky hlavní a vedlejší poloosy, je tzv. bodová konstrukce II. Její největší výhodou je fakt, že na konstrukci bodů nepotřebujeme kružítko.
Postup je nahraný v apletu E7.2. Dány jsou velikosti hlavní a vedlejší poloosy. Sestrojme vrcholy A, \, B, \, C, \, D hledané elipsy. Pro dohledání dalších bodů budeme potřebovat spojnice hlavních a vedlejších vrcholů. Hledejme např. body elipsy, které leží v kvadrantu určeném hlavní a vedlejší osou, jenž je incidentní se spojnicí AC. Nejprve zvolíme na úsečce AC libovolný bod L_1, jím vedeme polopřímku DL_1 (spojnici s druhým vedlejším vrcholem) a také rovnoběžku s hlavní osou o_1. Průnik této rovnoběžky a vedlejší osy o_2 označíme L_2. Bodem L_2 a druhým hlavním vrcholem B proložíme přímku L_2B. Průnik přímek L_1D a L_2B je hledaný bod I elipsy. (čerpáno z: Brejmann [14] str. 157 a 158)
Aplet E7.2: Bodová konstrukce elipsy II
Tato konstrukce však nevychází z definice elipsy, ale z afinního vztahu mezi kružnicí a elipsou. Pokud bychom měli alespoň naznačit důkaz, využívala by se v něm kružnice (afinní obraz elipsy) nad průměrem AB. Příslušná afinita by byla dána osou o = o_1 = AB a směrem kolmým k této ose. Snadno lze dokázat, že bodová konstrukce II platí pro danou kružnici a díky afinnímu vztahu tedy i pro elipsu.
Pozn.: Osová afinita v rovině je zobrazení, které zachovává poměry délek. Je nejčastěji zadána osou o a dvojicí odpovídajících si bodů A, \, A', která určuje směr afinity s. Je-li směr kolmý k ose o, nazývá se taková afinita pravoúhlá. Jestliže s \, || \, o, jedná se o afinní elaci. Odpovídající si body leží na přímce rovnoběžné se směrem afinity s, odpovídající si přímky se protínají na ose afinity o v tzv. samodružných bodech.
Zahradnická konstrukce
Zahradnická konstrukce vychází z vlastnosti konstantního součtu vzdáleností bodů od obou ohnisek elipsy stejně jako bodová konstrukce I. Má ovšem mnohem praktičtější využití v běžném životě. Např. jestliže si na zahrádce chceme udělat záhon tvaru elipsy, potřebujeme pouze jeden provázek délky 2a, dva pevné body F_1, \, F_2 (ohniska) - zapíchnuté kolíky a potom nějaké rydlo R, resp. křídu, propisku atd. Oba konce provázku přivážeme na kolíky F_1, \, F_2. Rydlem pak pohybujeme po napnutém provázku a vykreslíme křivku.
V apletu E7.3 si simulaci zahradnické konstrukce můžete vyzkoušet. Pohybujte "rydlem" R. Součet délek úseček F_1R, \, F_2R je konstantní, proto získáte elipsu.
Aplet E7.3: Zahradnická konstrukce elipsy
Konstrukce je do jisté míry amatérská a ne zcela přesná. Její výhodou je ovšem jednoduchost a praktičnost použití.
Rozdílová proužková konstrukce
Známe-li délku hlavní a vedlejší poloosy a, \, b můžeme pomocí proužku papíru najít body elipsy. Na okraj proužku papíru vyznačíme body L_1, \, L_2, \, L_3 (v tomto pořadí!, body leží v přímce) tak, že |L_1L_3| = a a |L_2L_3| = b. Narýsujeme osy o_1, \, o_2 elipsy. Proužkem papíru pohybujeme tak, aby bod L_1 zůstával na vedlejší ose o_2, bod L_2 na hlavní ose o_1. Bod L_3 určuje jednotlivé body křivky. Tedy, pohybujeme-li správně proužkem, bod L_3 vykreslí elipsu.
Model rozdílové proužkové konstrukce je v apletu E7.4. Pohybujte bodem L_1 po vedlejší ose o_2. Body L_1, \, L_2, \, L_3 jsou nastaveny tak, jak si konstrukce žádá. Bod L_3 vykresluje část elipsy k_e.
Aplet E7.4: Rozdílová proužková konstrukce elipsy
Máme-li sestrojit elipsu, která je zadána pouze hlavními vrcholy A, \,B a jedním bodem X, lze lehce dohledat délku vedlejší poloosy pomocí rozdílové proužkové konstrukce (a to i bez použití papírku). Konstrukce je nahrána v apletu E7.5.
Najdeme střed S elipsy (= střed AB) a vedlejší osu o_2 (kolmice vztyčená v bodě S na úsečku AB). Vedlejší vrcholy, které hledáme, budou s osou o_2 incidentní. Bod X představuje bod L_3 z rozdílové proužkové konstrukce. Sestrojíme kružnici k \, (X, \, a) a najdeme její průsečík L_1 s vedlejší osou o_2 tak, aby úsečka L_1L_3 protínala úsečku AB. Bod L_2 je průsečíkem L_1L_3 a AB. Díky nalezenému bodu L_2 můžeme dourčit délku vedlejší poloosy b = |L_2L_3|.
Aplet E7.5: Rozdílová proužková konstrukce elipsy II
Součtová proužková konstrukce
Proužkovou konstrukci lze provést ještě jedním způsobem (viz aplet E7.6). Opět si na proužek papíru přeneseme délku hlavní a vedlejší poloosy a, \, b pomocí kolineárních bodů L_1, \, L_2, \, L_3. Tentokrát ale |L_1L_2| = a a |L_2L_3| = b. Proužkem pohybujeme tak, aby bod L_1 zůstával na vedlejší ose o_2, bod L_3 na hlavní ose o_1. Bod L_2 určuje jednotlivé body křivky. Tedy, pohybujeme-li správně proužkem papíru, bod L_2 vykreslí elipsu.
Model součtové proužkové konstrukce je v apletu E7.6. Pohybujte bodem L_3 po hlavní ose o_1. Body L_1, \, L_2, \, L_3 jsou nastaveny tak, jak si konstrukce žádá. Bod L_2 vykresluje část elipsy k_e.
Aplet E7.6: Součtová proužková konstrukce elipsy
Naskýtá se znovu otázka, jak sestrojit elipsu, která je zadána pouze hlavními vrcholy A, \, B a jedním bodem X. Vedlejší vrcholy nyní dohledáme pomocí součtové proužkové konstrukce.
Najdeme střed S elipsy a vedlejší osu o_2. Vedlejší vrcholy, které hledáme, budou ležet na ose o_2. Bod X představuje bod L_2 ze součtové proužkové konstrukce. Pokud bychom situaci řešili pomocí papírku, přenesli bychom na něj velikost a = |L_1L_2|.Pak bychom bod L_2 na papírku přiložili přesně na bod X a bod L_1 nastavili tak, že bude ležet na o_2, přičemž bod L_3 by byl průnikem přímek L_1L_2 a AB. Délka |L_2L_3| by byla velikostí vedlejší poloosy b.
Přesnější je ovšem postup bez použití proužku papíru, který je nahrán v apletu E7.7. Sestrojíme kružnici k \, (X=L_2, \, a) a najdeme její průsečík L_1 s vedlejší osou o_2 tak, aby úsečka L_1L_2 neprotla úsečku AB. Bod L_3 je průsečíkem přímek L_1L_2 a AB. Tím jsme zjistili velikost vedlejší poloosy b = |L_2L_3| a elipsu dourčili.
Aplet E7.7: Součtová proužková konstrukce elipsy II
Trojúhelníková konstrukce
Trojúhelníková konstrukce je jedna z nejpřesnějších konstrukcí bodů elipsy. Využívá se zde složení dvou pravoúhlých osových afinit. (Pozn.: První afinita je mezi kružnicí k_1 \, (S, \, b), kde S je střed elipsy, a hledanou elipsou k_e, její osa je vedlejší osa elipsy. Druhá afinita je mezi kružnicí k_2 \, (S, \, a) a k_e, její osa je hlavní osa elipsy.)
Nechť je elipsa k_e zadána svými hlavními a vedlejšími vrcholy A, \, B, \, C, \, D. Známe tím také a = |AS| = |BS|, b = |CS| = |DS|, kde S je střed elipsy k_e. Sestrojíme kružnice k_1 \, (S, \, b), \; k_2 \, (S, \, a). Narýsujeme libovolnou přímku l procházející středem S. Ta protne každou z kružnic k_1, \, k_2 ve dvou bodech. Zvolíme jednu dvojici bodů l \cap k_1 = X_1, \, l \cap k_2 = X_2 takovou, že X_1, \, X_2 leží ve stejném kvadrantu určeném osami elipsy (viz aplet E7.8), resp. takovou dvojici bodů X_1, \, X_2, že každý z nich leží v jiném kvadrantu (viz aplet E7.9). Nyní si uvědomme, že kružnice k_1 se při pravoúhlé osové afinitě s osou o_2 (směr je kolmý k ose o_2) zobrazí na elipsu k_e. Kružnice k_2 se zobrazí na tutéž elipsu k_e při pravoúhlé osové afinitě určené osou o_1 (směr je kolmý k ose o_1). Tedy bod X elipsy k_e - obraz bodu X_1 budeme hledat na přímce rovnoběžné s hlavní osou o_1. Zároveň bod X bude obraz bodu X_2, tudíž bude ležet na rovnoběžce s vedlejší osou o_2. Různou volbou přímky l získáváme různé body elipsy k_e.
V apletu E7.8 a E7.9 jsou konstrukce nahrány. Po přehrání konstrukcí můžete měnit polohu přímky l pomocí bodu L a tím získat další body elipsy.
Aplet E7.8: Trojúhelníková konstrukce elipsy I
Aplet E7.9: Trojúhelníková konstrukce elipsy II
Pozn.: Konstrukce se nazývá trojúhelníková z prostého důvodu, jelikož při získávání bodů elipsy v rysu vznikají trojúhelníky, zde např. trojúhelník XX_1X_2.
Příčková konstrukce
Příčková konstrukce elipsy se využívá v rysech, kde je elipsa zadána omezenými sdruženými průměry a v nichž chceme elipsu dourčit bodově, sestrojit ji, ale nezajímají nás její hlavní ani vedlejší poloosy nebo jiné další prvky. Hojně se používá pro konstrukci kružnice ve středovém promítání - nejčastěji pro kružnici ve svislé rovině.
Nechť jsou dány omezené sdružené průměry KL, \, MN
elipsy k_e. Označme S jejich průsečík - střed elipsy. Sestrojíme rovnoběžník OPQR tak, že KL, \, MN představují jeho střední příčky. Jedná se o rovnoběžník, který bude elipse k_e opsaný.
Pro jednoduchost se zaměříme jen na jeden kvadrant určený sdruženými průměry KL, \, MN, nechť je to kvadrant určený body K, \, S, \, N, \, R. Nyní rozdělíme úsečku SN na libovolný počet shodných dílů (v apletu E7.10 jsou to čtyři shodné díly) a dělící body očíslujeme ve směru od bodu S k bodu N. Na tentýž počet shodných dílů rozdělíme i úsečku RN a dělící body očíslujeme postupně od bodu R k bodu N. Dělícími body na úsečce SN jsou vedeny přímky procházející bodem L a dělící body na úsečce RN jsou spojeny s bodem K. Příčky, které vycházejí z bodů s odpovídajícími si čísly, se protínají v bodech elipsy k_e. Obdobně bychom provedli konstrukci i ve zbývajících kvadrantech.
V apletu E7.10 je konstrukce nahrána, stačí ji spustit tlačítkem "Přehrát".
Aplet E7.10: Příčková konstrukce elipsy
Rytzova konstrukce
Rytzova konstrukce se používá v případech, kdy známe dvojici sdružených omezených průměrů elipsy a potřebujeme dohledat hlavní a vedlejší poloosy (viz aplet E7.11).
Je to velice často používaná, "standardní" konstrukce, proto pro zájemce je uveden i její důkaz. Sám autor, švýcarský matematik a učitel D. Rytz (1801 - 1868), sice konstrukci vymyslel, ale důkaz k ní již nedoložil. Konstrukce byla dokázána později, a to L. Mossbrugerem Rytzovým kolegou. Konstrukce je z roku 1845.
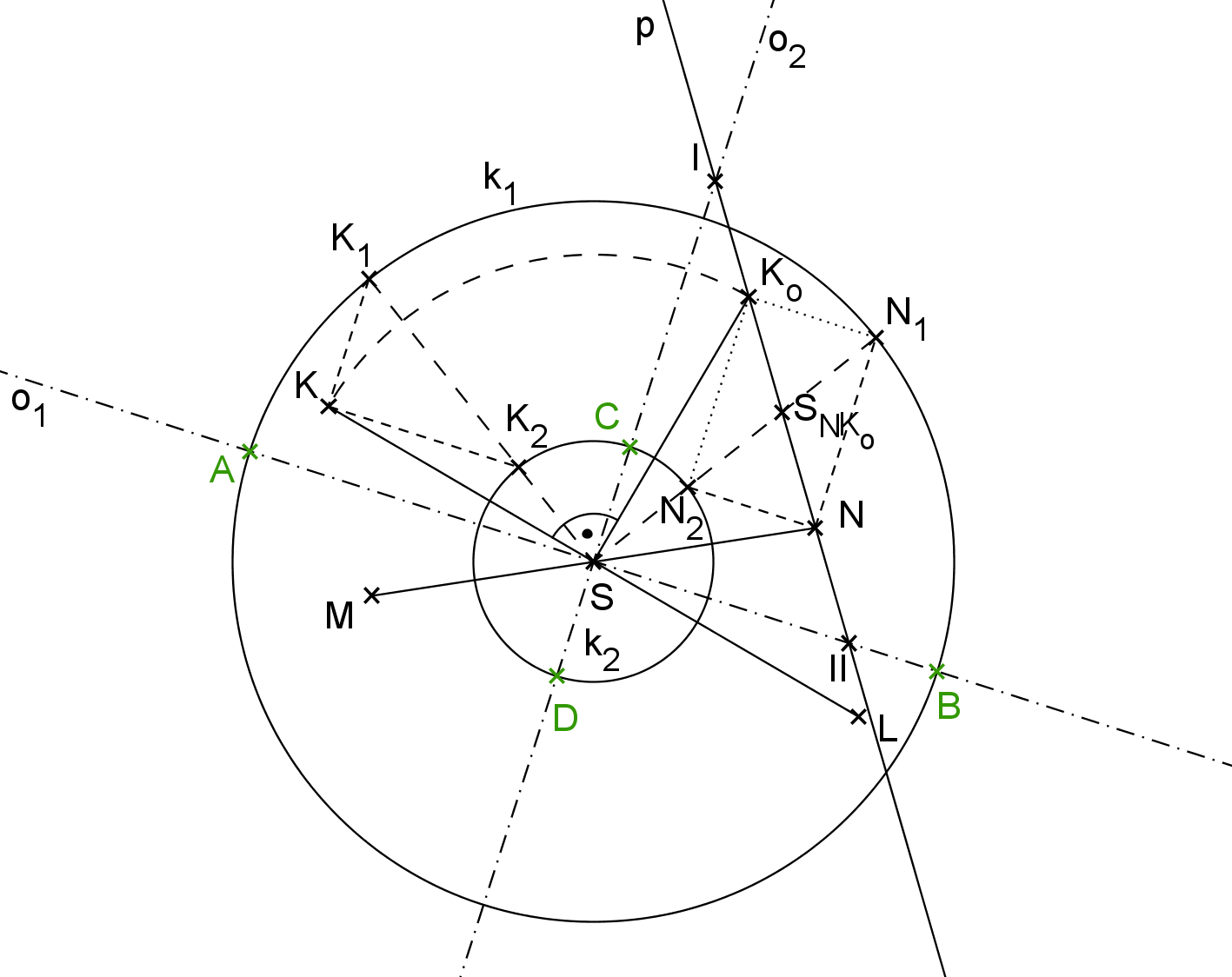
Nechť jsou dány omezené sdružené průměry KL, \, MN. Jejich průsečík S je středem hledané elipsy k_e. Zvolíme jeden z koncových bodů průměru, nechť je to K, a otočíme ho kolem středu S o 90^o. Otočeným bodem K_o vedeme přímku p, která též prochází bodem N - bodem průměru sdruženého. Dále najdeme střed S_{NK_o} úsečky NK_o a sestrojíme kružnici k \, (S_{NK_o}, \, |SS_{NK_o}|), která protne přímku p ve dvou bodech I a II. Jsou to body, jimiž prochází osy elipsy. Velikost hlavní a vedlejší poloosy nalezneme na přímce p, platí: |IN| = a, \; |NII| = b. Stačí už jen vynést délky a, \, b ve správném pořadí na osy o_1, \, o_2.
Aplet E7.11: Rytzova konstrukce elipsy
Pro zájemce konstrukci ozřejmí následující důkaz:
Důkaz: (obrázek E7.1)
Nechť je dána elipsa k_e svými hlavními a vedlejšími vrcholy A, \, B, \, C, \, D. Sestrojme kružnice k_1 \, (S, \, a) a k_2 \, (S, \, b), kde S je střed elipsy k_e. Jak již bylo řečeno, daná elipsa je afinním obrazem kružnice k_1 a také k_2 (jde o speciální případ pravoúhlých osových afinit s osami totožnými s osami elipsy k_e).
Zvolme dva navzájem kolmé poloměry SK_1, \, SN_1 kružnice k_1. V pravoúhlé afinitě s osou o_1 jim odpovídají sdružené poloměry SK, \, SN. Označíme-li K_2, \, N_2 průsečíky obou kolmých průměrů s kružnicí k_2, pak jsou trojúhelníky N_2NN_1, \, K_1KK_2 shodné, neboť |N_2N_1| = |K_2K_1|, \, N_2N_1 \perp K_2K_1, \, NN_1 \perp K_2K. Otočíme-li trojúhelník K_1KK_2 okolo středu S o 90^o, bod K_2 splyne s bodem N_2, bod K_1 s bodem N_1 a bod K se otočí do bodu K_o. Bod K_o je zároveň čtvrtým vrcholem obdélníka N_1NN_2K_o. Označme I a II průsečíky jeho úhlopříčky NK_o s vedlejší a hlavní osou. Z rovnoběžnosti N_1N \parallel K_oN_2 \parallel CS, \, N_2N \parallel K_oN_1 \parallel SB vyplývá rovnost úseček:
|SN_1| = |NI| = |K_oII| = a,
|SN_2| = |NII| = |K_oI| = b.
Obrázek E7.1: Rytzova konstrukce - důkaz
Frézierova konstrukce
A. D. Frézier (1682 -1773) byl bez pochyby nejpozoruhodnější vědec 18. století. Působil ve francouzském městě Savoie, ale původem pocházel ze Skotska, jeho originální jméno bylo Frazer. Mnozí ho považují za zakladatele deskriptivní geometrie.
(čerpáno z [W5])
Frézierova konstrukce (viz aplet E7.12) je o více než sto let starší než Rytzova konstrukce, pochází z roku 1737. Z našeho pohledu ovšem bude jen jakýmsi zvláštním provedením konstrukce Rytzovy.
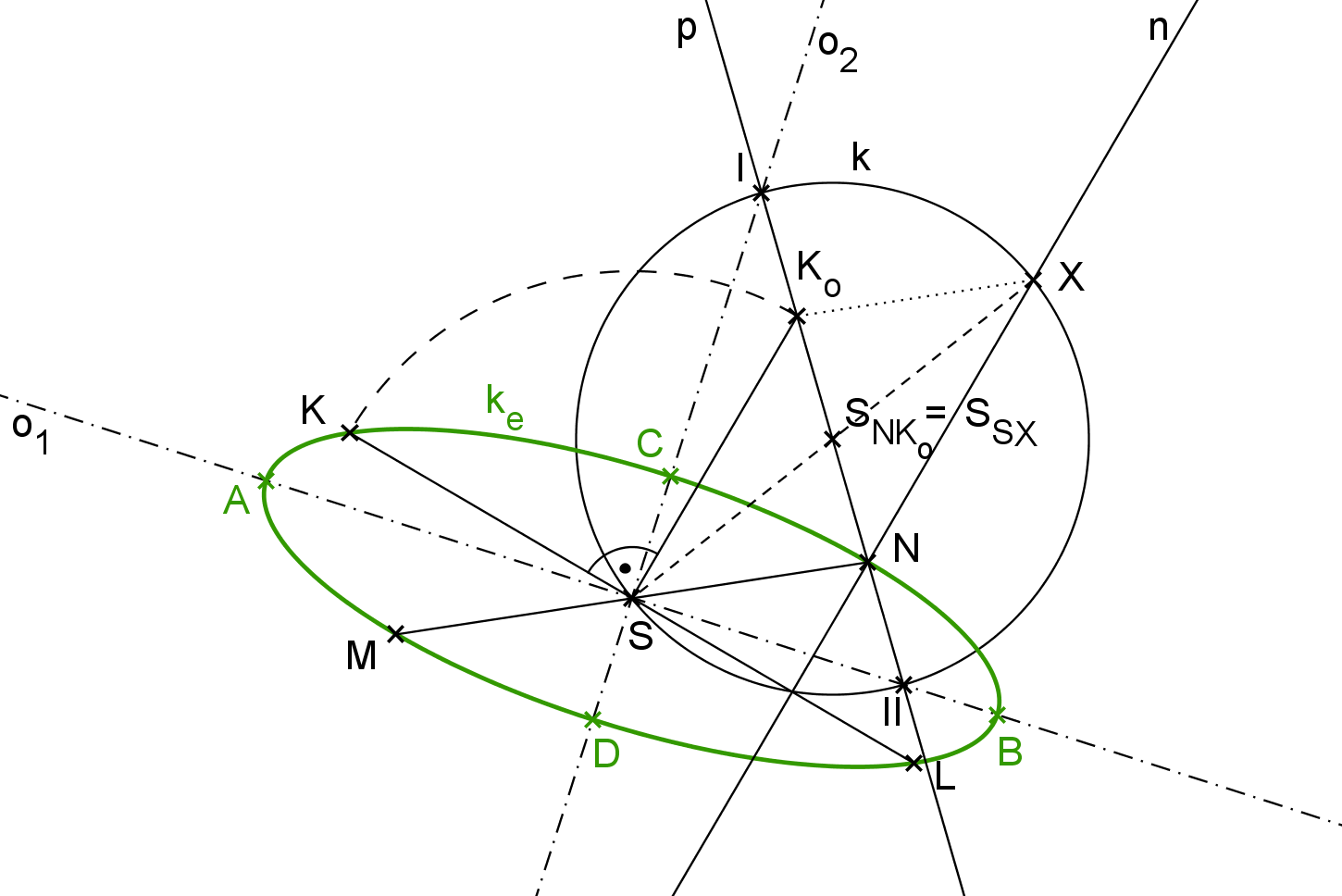
Nechť jsou dány omezené sdružené průměry KL, \, MN. Jejich průsečík označme S, je to střed hledané elipsy k_e. Z koncového bodu N kratšího průměru spustíme kolmici n na úsečku SL. Na kolmici n najdeme bod X, pro který platí: |NX| = |SL| = |SK| tak, že bod N leží mezi patou kolmice n a bodem X. Sestrojíme střed S_{SX} úsečky SX. Tím získáme bod, jenž je totožný se středem S_{NK_o} z Rytzovy konstrukce. Dále tedy budeme postupovat úplně stejně jako u Rytzovy konstrukce. Sestrojíme kružnici k \, (S_{SX}, \, |SS_{SX}|) a přímku p = NS_{SX}, jejich průnikovými body I, \, II procházejí osy o_1, \, o_2 elipsy k_e. Délku hlavní a vedlejší poloosy odečteme na přímce p: |NI| = a, \, |NII| = b.
Frézierova konstrukce elipsy je nahrána v apletu E7.12, kde se můžete podívat na odkrokovaný postup.
Aplet E7.12: Frézierova konstrukce elipsy
Pozn.: Již na začátku bylo řečeno, že tato konstrukce je ve své podstatě zvláštním případem Rytzovy konstrukce. Přesvědčíme se o pravdivosti tohoto tvrzení.
Stačí dokázat, že střed S_{SX} z Frézierovy konstrukce je totožný se středem S_{NK_o} z konstrukce Rytzovy. Pokud obě konstrukce narýsujeme dohromady, vznikne rys, jenž je na obrázku E7.2. V rysu vznikl čtyřúhelník SNXK_o. Dokážeme-li, že se jedná o rovnoběžník, dokážeme tím totožnost středů S_{SX} a S_{NK_o}.
Zřejmě úsečky SK_o a NX jsou rovnoběžné, protože obě jsou kolmé na úsečku KL. Také mají stejné délky: |NX| = |SK| = |SK_o|. Z těchto dvou vlastností už přímo plyne rovnoběžnost a shodnost délek úseček SN a K_oX, platí tedy: S_{SX} = S_{NK_o}.
Obrázek E7.2: Frézierova versus Rytzova konstrukce
Konstrukce elipsy ohýbáním papíru
Jedna z netypických konstrukcí je určitě konstrukce elipsy ohýbáním papíru. Pokud známe hodnotu excentricity e a hlavní poloosy a, můžeme ji použít.
Nejlépe na průhledný papír (tzv. "pauzák") narýsujeme kružnici k se středem v libovolně zvoleném bodě F_1 a poloměrem 2a. Druhý bod F_2 zvolíme tak, že platí: |F_1F_2| = 2e (viz. obrázek E7.3 a)). Nyní budeme ohýbat papír tak, aby vždy ohnutá část kružnice k procházela bodem F_2. Přesně jak je tomu na obrázku E7.3 b).
Každý ohyb je v podstatě tečnou elipsy. Dostáváme tedy množinu tečen (viz obrázek E7.3 c), d)), které žádanou elipsu obalují. Výsledek je na obrázku E7.4.
Obrázek E7.3: Konstrukce elipsy ohýbáním papíru

Obrázek E7.4: Výsledná elipsa
Pozn.: Pro sestrojení elipsy si jistě tuto konstrukci volit nebudeme. Má ovšem jiný účel, demonstruje funkci ohniskových vlastností elipsy. Konkrétně se jedná o větu E3.2 a větu E4.1 (kapitoly Tečny a normály elipsy) a Ohniskové vlastnosti elipsy). Kružnice k představuje řídicí kružnici opsanou z ohniska F_1. Je tedy množinou všech bodů souměrně sdružených s druhým ohniskem F_2 podle tečen elipsy - ohybů papíru.